Il triangolo equilatero è un particolare tipo di triangolo con i 3 lati e i 3 angoli tutti uguali. Rientra quindi nella categoria dei poligoni regolari e viene chiamato anche triangolo equiangolo.
In questa lezione vedremo come si fa a calcolare l’area del triangolo equilatero, il perimetro e analizzeremo tutte le formule e le proprietà di questa figura geometrica piana. Per quanto riguarda le formule, restano valide quelle studiate nella teoria del triangolo scaleno.
Triangolo equilatero definizione
Come già detto nella parte introduttiva, il triangolo equilatero è un poligono regolare avente 3 angoli e lati congruenti, cioè uguali.
Formule triangolo equilatero
Vediamo a questo punto tutte le forme che riguardano questa particolare figura piana, partendo dalle più semplici ed elementari per perimetro ed area fino a quelle più complesse, che difficilmente trovi sui libri.
Sia dato allora un triangolo equilatero generico, indichiamo con p la misura del perimetro, sia invece A l’area, H l’altezza e L la misura del lato.
Formule elementari
Perimetro triangolo equilatero
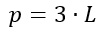
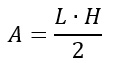
Con le formule inverse puoi quindi calcolare quindi lato ed altezza avendo a disposizione area o perimetro.
E’ importante premettere che se sei uno studente delle scuole medie o elementari, è preferibile attenerti alle formule base, visto che quelle avanzate fanno riferimento a programmi non ancora trattati.
In tuo aiuto, però, c’è la formula del Teorema di Pitagora che potrai utilizzare: una volta tracciata l’altezza hai infatti 2 triangoli rettangoli su cui lavorare.
Formule avanzate
Altezza noto il lato
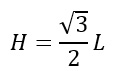
Area avendo solo il lato
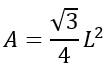
Apotema triangolo equilatero
(raggio circonferenza inscritta)
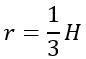
Raggio circonferenza circoscritta
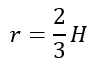
Approfondimenti: Triangolo equilatero inscritto in una circonferenza
Proprietà del triangolo equilatero
Ecco riassunte tutte le caratteristiche di questo particolare tipo di triangolo:
- ha tutti i lati uguali;
- ha tutti gli angoli uguali e misurano 60°. Anche per questo è un particolare tipo di triangolo acutangolo;
- è sempre inscrivibile in una circonferenza;
- è un particolare tipo di triangolo isoscele;
- l’altezza divide la figura in due triangoli rettangoli da 30 60 90;
- poiché lati ed angoli sono tra loro uguali, mediana, asse e bisettrice coincidono;
- coincidono quindi anche ortocentro, incentro e baricentro;
Esercizi svolti
A questo punto ti consigliamo di risolvere un po’ di esercizi sui triangoli equilateri. Eccone alcuni svolti.
Problema 1
Il perimetro del triangolo equilatero misura 180 cm. Calcola la misura dei lati.
SVOLGIMENTO
Perimetro triangolo equilatero formula: P=3L
Eseguendo la formula inversa, sappiamo che un lato è il perimetro diviso 3. Quindi L=180/3= 60 cm.
Problema 2
Calcola l’area del triangolo equilatero con lato pari a 8 cm.
Svolgimento
Poiché abbiamo solo il lato a disposizione e dobbiamo calcolare l’area, possiamo usare la formula diretta vista in alto procedere un passo alla volta (consigliato per studenti delle scuole medie).
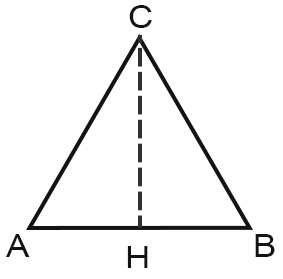
Sappiamo che AH=AB/2, quindi AH=8/2= 4 cm
Consideriamo il triangolo rettangolo AHC e applichiamo il teorema di Pitagora per calcolare l’altezza. HC è il cateto maggiore da calcolare, AC è l’ipotenusa che misura 8 cm, AH il cateto minore che misura 4 cm.
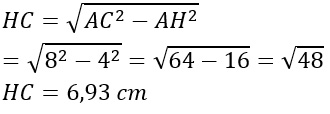
A questo punto basta calcolare base per altezza diviso due e troveremo:
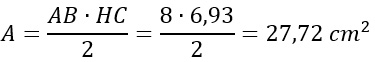
Problema 3
Un rettangolo ha perimetro da 45,8 cm e l’altezza misura 1,45 cm più del doppio della base. Calcola il perimetro del triangolo equilatero che ha lato pari al doppio della dimensione minore del rettangolo.
SVOLGIMENTO
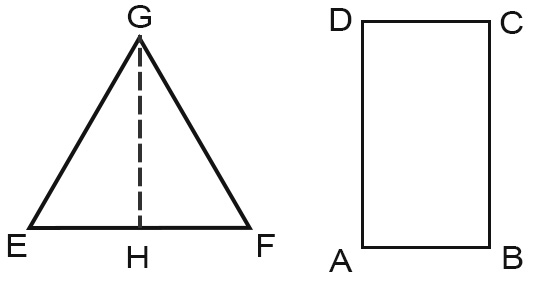
Mentre gli studenti delle superiori possono risolvere comodamente risolvere l’esercizio con la x e le equazioni di primo grado, gli studenti delle scuole medie devono risolvere sfruttando le unità equivalenti (u).
In questo tipo di esercizio vale sempre la pena ricavare, dove possibile, la somma delle due incognite, base e altezza del rettangolo. Avendo il perimetro del rettangolo, sappiamo che la somma di base e altezza è pari al semiperimetro. Quindi AB+BC=45,8/2=22,9 cm.
Poiché BC è più grande di AB, disegniamo quest’ultimo come un segmento di lunghezza u. Quindi AB e BC li posso disegnare come:
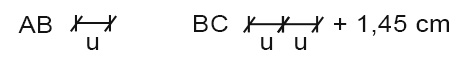
So a questo punto che la loro somma è 22,9 cm, per cui posso rappresentarla graficamente:
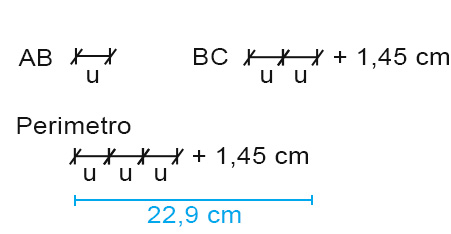
Da notare che se al segmento blu da 22,9 (il semiperimetro) tolgo 1,45, mi restano 3u. Per cui:
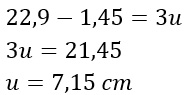
Per cui possiamo calcolare la misura dei due lati:
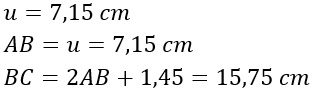
La traccia ci dice ora che il lato è pari al doppio della misura del lato minore del rettangolo. Per cui EF=2AB=14,3 cm.
Possiamo quindi chiudere l’esercizio e calcolare il perimetro del triangolo equilatero semplicemente moltiplicando il lato per 3.
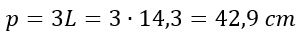
Conclusioni
Abbiamo visto in questa lezione quali sono le proprietà e le formule del triangolo equilatero. Ci siamo esercitati con problemi con un livello di difficoltà crescente e ora siamo pronti ad affrontare davvero qualsiasi tipo di esercizio.
La lezione ti è stata utile o hai anche qualche dubbio? Lasciaci un feedback o una domanda nei commenti. Ci aiuterai a migliorare la qualità delle lezioni.