Il trapezio scaleno è un quadrilatero formato da due lati paralleli detti basi e due lati obliqui di misura diversa. E’ un poligono molto importante nel programma di geometria e di cui bisogna conoscere almeno le formule generali, visto che tra tutti i tipi di trapezi è quello più utilizzato.
Avendo già trattato caratteristiche e formule del trapezio generico in un’altra lezione, su questa pagina vedremo una spiegazione sul trapezio scaleno più specifica, analizzandone formule e proprietà. Iniziamo vedendo subito che cos’è questa figura geometrica.
Trapezio scaleno definizione
Lascia perdere Wikipedia e cerchiamo di mantenerci su concetti facili da capire e da applicare. Come già detto all’inizio di questa lezione, il trapezio scaleno è un poligono formato da 4 lati, due dei quali sono paralleli e prendono il nome di basi. Gli altri due hanno lunghezza diversa e si chiamano lati obliqui.
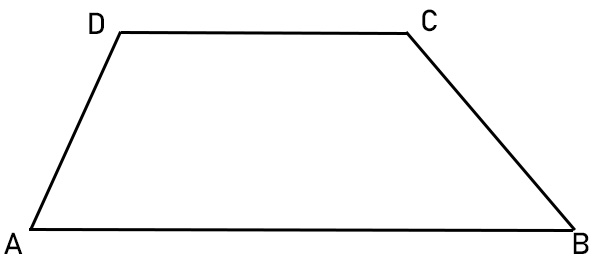
Quindi in base alla definizione, dato il trapezio scaleno ABCD in figura, sappiamo che le due basi AB e CD sono parallele. Quella più lunga si definisce base maggiore (AB), mentre l’altra si definisce base minore (CD).
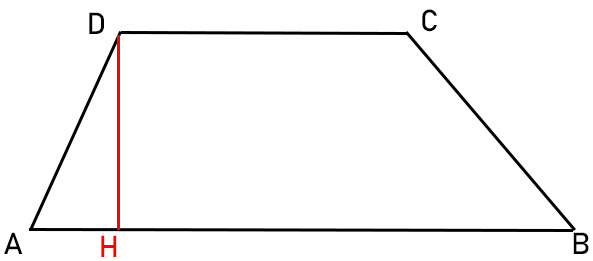
La distanza tra le due basi si chiama altezza del trapezio scaleno e il punto che forma sulla base viene indicato generalmente con la lettera maiuscola H.
Trapezio scaleno formule
In questo capitolo vedremo tutte le formule e le formule inverse che riguardano questa particolare figura geometrica. Analizziamole una ad una…
Area trapezio scaleno
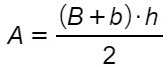
L’area del trapezio scaleno si calcola facendo la somma delle basi, per l’altezza diviso due. Dalle formule inverse possiamo ricavare le basi o l’altezza.
Approfondimenti: Area trapezio isoscele | Area trapezio rettangolo
Formule inverse
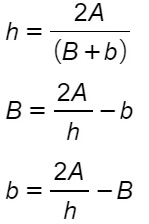
Trapezio scaleno perimetro
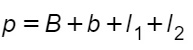
Il perimetro del trapezio scaleno si calcola semplicemente sommando tutti i lati della figura. Per usare le formule inverse, servirà il perimetro e la misura di 3 lati.
Formule inverse
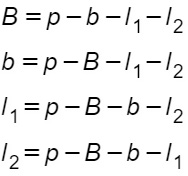
Proprietà del trapezio scaleno
- La somma degli angoli interni di un trapezio scaleno vale 360°, cioè è pari ad un angolo giro.
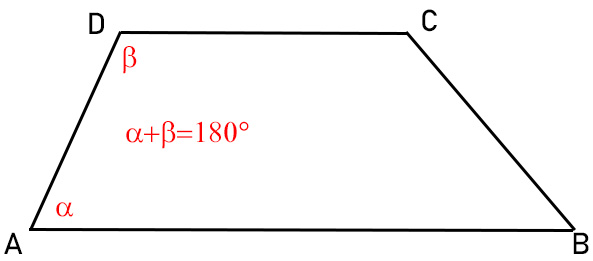
- I due angoli adiacenti a ciascun lato obliquo sono supplementari.
- I lati obliqui hanno lunghezza diversa.
- Gli angoli alla base del trapezio scaleno non sono congruenti.
- Le diagonali di un trapezio scaleno non sono uguali tra loro.
- Se uno dei lati obliqui è perpendicolare alla base, allora la figura diventa un trapezio rettangolo.
- Disegnando l’altezza di ottengono due figure più semplici: un triangolo rettangolo e un trapezio rettangolo.
- Disegnando le due altezze si ottengono 3 figure più semplici: due triangoli rettangoli (diversi tra loro) e un rettangolo.
Esercizi svolti
Problema 1
Calcolare la misura delle basi di un trapezio scaleno con perimetro pari a 182 cm, lati obliqui pari a 31,5 e 45,5 cm, sapendo che la base maggiore supera la base minore di 49 cm.
Svolgimento
Gli studenti delle scuole superiori possono risolvere il problema di geometria utilizzando l’incognita x e svolgendo una semplice equazione di primo grado.
Per gli studenti delle scuole medie consigliamo invece di ragionare disegnando dei segmenti. Immagina che B e b, le due basi, possano essere disegnati con due segmenti di misure differenti. Non importa quanto farli lunghi.

Sappiamo a questo punto che la somma dei due è 182-31,5-45,5 cm, cioè 105 cm. Matematicamente possiamo scrivere B+b=182 cm che graficamente possiamo rappresentare come:
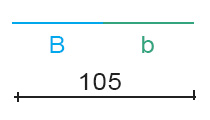
Sappiamo inoltre che la base maggiore supera la minore di 49 cm. Cioè matematicamente possiamo scrivere che B=b+49 cm. Dal punto di vista grafico diventa:
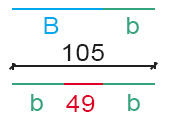
Al posto del segmento blu (B) abbiamo messi b (in verde) più i 49 cm (in rosso). Possiamo notare che se dai 105 totali sottraiamo il segmento rosso, quindi togliamo 49 cm, restano solo i due segmenti blu, cioè 2 volte b. Quindi possiamo scrivere:
105-49=2b da cui ricaviamo:
2b=105-49
2b=56 e da cui ricavo b=28.
Quindi B=b+49=28+49 –> B=77 cm.
Problema 2
Dati un trapezio scaleno e un triangolo isoscele tra loro isoperimetrici, con perimetro pari a 55 cm. La base del triangolo è 3/4 del lato obliquo. Per quanto riguarda il trapezio sappiamo che il lato obliquo misura 13 cm mentre la somma delle basi è uguale al lato obliquo del triangolo. Trova la misura dell’altro lato obliquo del trapezio
Svolgimento
Per gli studenti delle scuole medie consigliamo di risolvere attraverso le unità (u), come ogni volta che c’è un rapporto tra lati. Scriviamo innanzitutto i dati del problema.
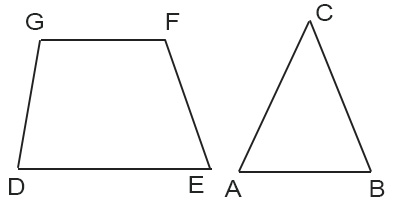
Dati del triangolo isoscele:
p=55 cm
AB+2BC=55 cm
AB=3/4 BC
Dati del trapezio scaleno:
p=55cm
EF=13 cm
DE+FG=BC
INCOGNITA: DG=?
Svolgimento: Iniziamo risolvendo il triangolo. Conoscendo il perimetro, sappiamo quindi quanto vale la somma di tutti i lati, cioè:
AB+BC+AC=55 cm, dove AB=3/4 BC
Questo vuol dire che se dividiamo AB in un segmento composto da 4 piccoli pezzettini tutti uguali (chiamate anche unità), vuol dire che AB=4u mentre AB=3u
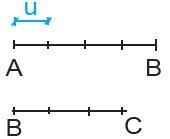
Poiché i lati obliqui del triangolo sono uguali, il perimetro possiamo anche scriverlo come:
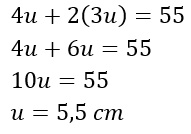
Quindi possiamo calcolare le misure dei lati:
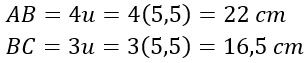
Poiché la traccia sottolinea che la somma della basi del trapezio scaleno è pari al lato obliquo del triangolo, allora DE+GF=16,5 cm.
Sfruttiamo la formula del perimetro del trapezio per calcolare l’incognita, ovvero il lato obliquo sconosciuto.
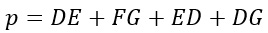
Per cui possiamo fare la formula inversa e calcolare il lato obliquo:
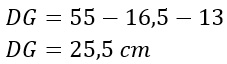
Conclusioni
Se la lezione ti è stata utile o se hai un problema da proporre, lascia un commento in basso. Ci aiuterai a migliorare la qualità delle nostre lezioni venendo sempre più incontro alle tue necessità.