Come si calcola il perimetro del rettangolo? Esistono formule alternative per poter trovare il perimetro di un rettangolo partendo dall’area o dalla diagonale?
In questa lezione faremo un approfondimento mirato sulle tecniche di calcolo del perimetro di calcolo, valutando non solo tutte le possibili formule (e formule inverse), ma anche risolvendo assieme alcuni semplici problemi di geometria.
Formule perimetro rettangolo
Il perimetro di un rettangolo rappresenta l’estensione totale dei bordi della figura geometrica. E’ possibile calcolarlo, usando la formula generale, cioè si sommano tutti lati.
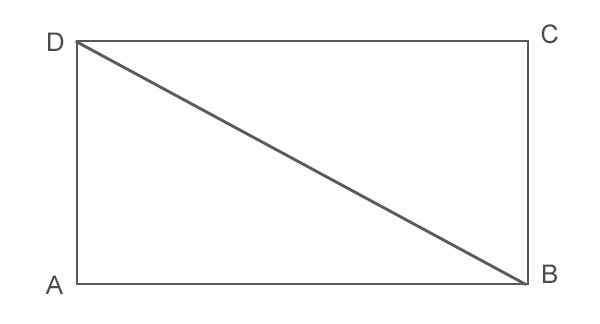
Poiché il rettangolo ha i lati uguali a 2 a 2, allora possiamo calcolare il perimetro sommando il doppio della base con il doppio dell’altezza.
Formula perimetro rettangolo
p=2b+2h
Dove p rappresenta la misura del perimetro del rettangolo, b è la base AB, mentre h è l’altezza AD. Su alcuni libri di testo il perimetro viene indicato anche con il simbolo 2p.
La formula appena vista è sicuramente quella più utilizzata e permette di trovare, in un generico rettangolo, il perimetro noto il lato.
Formule inverse
Applicando le formule inverse è possibile trovare la misura di base o altezza noto il perimetro e l’altro lato.
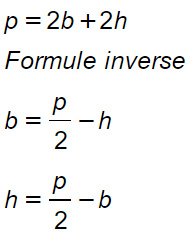
Esempio
Dato il rettangolo con perimetro 16 cm e base pari a 3 cm, calcolarne la base
Svolgimento
Usiamo le formule inverse per trovare subito l’altezza.
h=p/2-b
h=16:2-3= 8-3= 5 cm.
Come si risolve un problema però, se è nota la diagonale o l’area del rettangolo?
Calcolo perimetro rettangolo data l’area
Per poter risolvere il problema è necessario avere a disposizione anche un’altro dato: l’area da sola non è sufficiente. La traccia deve quindi darci la base o l’altezza (o almeno darci un modo per calcolare una delle due).
In questo modo si usa la formula inversa dell’area per trovare il lato mancante e poi si applica la formula per calcolare il perimetro del rettangolo.
Esempio
Calcolare il perimetro del rettangolo di area 96 cm2 e la base pari a 12 cm.
Svolgimento
Per risolvere l’esercizio, inizio calcolando l’altezza.
A=b·h → h=A:b → h=96:12= 8 cm
Una volta note base e altezza, possiamo calcolare il perimetro del rettangolo:
p=2b+2h
p=2(8 cm)+2(12 cm) = 16+24 = 40 cm.
Calcolo perimetro rettangolo nota la diagonale
Come nel caso precedente, la sola misura della diagonale del rettangolo non è sufficiente per determinare il perimetro. La traccia deve fornire un ulteriore dato: nella più semplice delle ipotesi ci fornirà uno dei due lati (base o altezza).
Se l’esercizio è più complesso e prevede l’uso di equazioni o dell’incognita x (non adatto a studenti delle scuole medie), allora può indicare anche nella traccia area o perimetro.
Problema risolto
Trovare il perimetro di un rettangolo che ha la diagonale che misura 20 cm e la base 10 cm.
Svolgimento

Per trovare l’altezza dobbiamo considerare il triangolo rettangolo ABD che si forma grazie alla diagonale AC. La diagonale è la sua ipotenusa, mentre la base è il cateto maggiore.
Possiamo applicare il teorema di Pitagora:
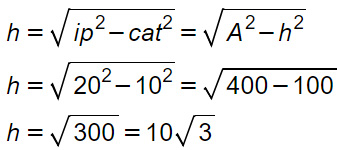
A questo punto, nota base e altezza, è possibile trovare la misura del perimetro.
p=2b+2h
p=2(10√3 cm)+2(10 cm) = 20√3+20 = 20(1+√3) cm.
Conclusioni
Abbiamo visto in questa lezione come trovare il perimetro del rettangolo noti i lati, oppure l’area o la diagonale. C’è unica formula da imparare e da cui si possono ricavare due formule inverse.
Se la lezione ti è stata d’aiuto, lascia un tuo commento/feedback in basso. Ci aiuterà a crescere e a fornirti ogni giorno nuove lezioni gratuite.
bravo