Categoria: Circonferenza e cerchio

Circonferenza e cerchio sono una parte fondamentale del programma di geometria. Mentre la circonferenza è l’insieme dei punti equidistanti dal centro, il cerchio è l’area racchiusa dalla circonferenza.

Spesso si fa confusione tra cerchio e circonferenza, in realtà la prima è un’area, mentre il secondo rappresenta il contorno della figura geometrica.

In questa pagina vedremo un formulario completo su circonferenza e cerchio. Partendo dalle definizioni, faremo un elenco di tutte le formule del cerchio con alcuni riferimenti sulle formule inverse.

Attenzione: questa lezione è dedicata anche agli studenti delle scuole primarie. Per un’analisi completa della circonferenza nel piano cartesiano, ti  consigliamo di consultare la sezione sulla geometria analitica.

Definizione di circonferenza e cerchio

Nell’introduzione di questa lezione abbiamo già risposto alla domanda “che cos’è la circonferenza?” Vediamo nel dettaglio:

• si definisce circonferenza l’insieme dei punti del piano equidistanti da un punto fisso detto centro;
• si definisce cerchio l’area del piano racchiusa all’interno della circonferenza.

Altre definizioni: raggio, centro, diametro, corda…

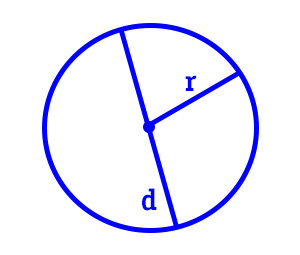
Come detto, il centro rappresenta il punto equidistante da tutti i punti della circonferenza. Proprio la distanza dal centro da uno qualunque dei punti della circonferenza si chiama raggio.

La corda è invece il generico segmento che unisce due generici punti della circonferenza. Il diametro, infine, è la corda massima, cioè è la corda che passa per il centro. Dal punto di vista dimensionale, il diametro è il doppio del raggio.

Si definisce arco della circonferenza, quella porzione di quest’ultima compresa tra due raggi. L’area invece compresa tra due raggi viene chiamata settore circolare.

Formule cerchio e circonferenza

Data la circonferenza lunga C di raggio r, diametro d, si indichi con la lettera A l’area del cerchio. Ecco di seguito elencate le principali formule della circonferenza e del cerchio.

• Formula del diametro

• Formula del raggio

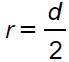
• Formula della circonferenza

• Area del cerchio

Attraverso le formule inverse è possibile ottenere la formula per calcolare il raggio nota la circonferenza o l’area.

Proprietà della circonferenza

1. Per tre punti non allineati passa una e una sola circonferenza.
2. Il diametro è la corda massima, cioè di dimensione maggiore.
3. Ogni angolo al centro è doppio rispetto agli angoli che si formano sulla circonferenza.
4. E’ sempre possibile inscrivere e circoscrivere una circonferenza in un poligono regolare.
5. Qualsiasi tipo di triangolo sia inscritto in una semicirconferenza è un triangolo rettangolo.

La posizione della retta rispetto alla circonferenza

Si tratta di un argomento che verrà approfondito nel programma di geometria analitica (vedi la lezione retta tangente alla circonferenza passante per un punto dato). Per ora ci accontentiamo di conoscere le definizioni.

Una retta è tangente alla circonferenza quando ha con quest’ultima 1 punto in comune. Si dice secante, quando i punti in comune sono 2. Si dice esterna quando non ci sono punti in comune.

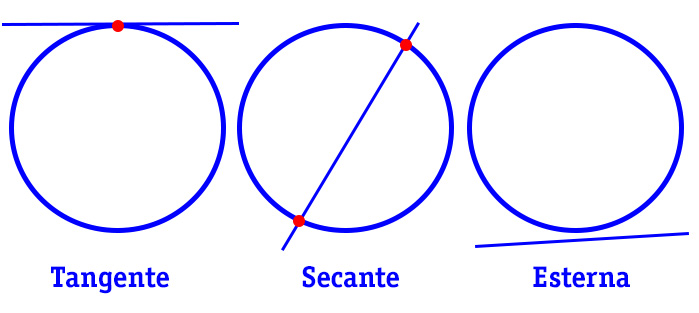
Ovviamente le definizioni sono del tutto analoghe se consideriamo la posizione di due circonferenze. Anche in tal caso possono essere esterne, tangenti o secanti a seconda che hanno 0, 1 o 2 punti in comune.

Approfondimenti

Di seguito trovi tutti i vari le varie lezioni di approfondimento che abbiamo dedicato alla circonferenza. Clicca per leggere la lezione che ti interessa…