Il teorema di Pitagora è uno dei più famosi teoremi della geometria e che si studia anche nella scuola primaria. La sua formula riguarda i triangoli rettangoli e consente di calcolare uno dei lati avendo a disposizione gli altri due.
Teorema di Pitagora formula
Dato il generico triangolo rettangolo ABC, su di esso individuiamo l’ipotenusa i, il cateto maggiore C e il cateto maggiore c. Vale la relazione:
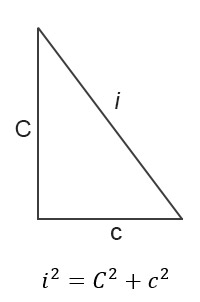
Ricordiamo che l’ipotenusa è il lato opposto all’angolo retto, mentre gli altri due lati vengono definiti cateto maggiore e cateto minore. Troverai su tutti i libri di matematica la definizione rigorosa che porta alla formula del Teorema di Pitagora.
Enunciato Teorema di Pitagora
DEFINIZIONE
In qualsiasi triangolo rettangolo, la somma dei quadrati costruiti sui cateti è pari al quadrato costruito sull’ipotenusa.
Che cosa vuol dire? Che possiamo letteralmente disegnare un quadrato su ogni lato così come nella figura che segue.
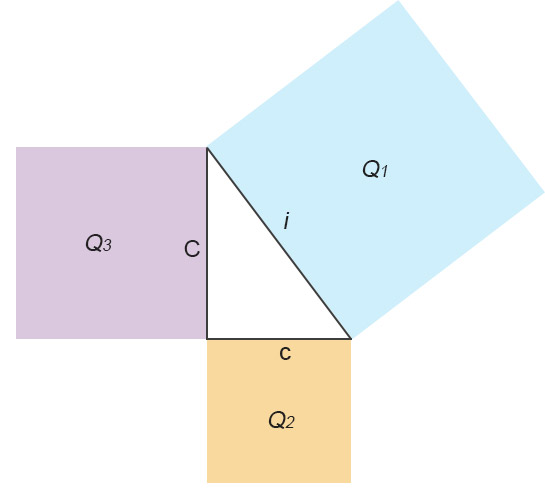
Ricordi come si calcola l’area del quadrato? Pitagora dimostrò che l’area di Q1 – cioè l’area del quadrato costruito sull’ipotenusa – è uguale a Q2+Q3, cioè la somma dell’area dei quadrati costruiti sui cateti.
Formule teorema di Pitagora
Una volta vista l’equazione principale da soddisfare, possiamo fare riferimento alle formule inverse per calcolare non solo l’ipotenusa, ma anche i due cateti. Ci saranno utilissime nello svolgimenti dei problemi. Ecco quando e come usarle:
- Formula inversa per calcolare il cateto minore, nota l’ipotenusa e il cateto maggiore
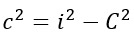
- Formula inversa per calcolare il cateto maggiore, nota l’ipotenusa e il cateto minore
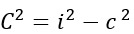
Come puoi vedere tutte hanno un termine al quadrato, per cui per completare la risoluzione ti è sufficiente applicare al primo e al secondo membro una radice quadrata.
Formulario completo
Riassumiamo quindi tutte le formule del teorema di Pitagora che abbiamo visto fino a questo momento, applicando anche la radice.
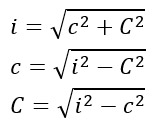
Applicazione della formula di Pitagora – esempio
Esempio 1) Calcolare l’ipotenusa di un triangolo rettangolo in cui i cateti sono uguali 4 e 5 cm.
Semplicemente applichiamo la formula del teorema di Pitagora:
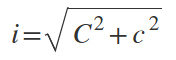
dove
c = cateto minore = 4 cm
C = cateto maggiore = 5 cm
i = √(4^2+5^2)=√(9+16)=√25
i=5
Esempio 2) Dato il triangolo isoscele di perimetro 64 cm e base 24 cm. Calcolare l’area del triangolo.
Poiché il triangolo isoscele ha due lati uguali possiamo riscrivere la formula del perimetro come:
p=l1+l2+l3 dove l2=l3
p=l1+2l2
Poiché abbiamo il perimetro e un lato applichiamo la formula inversa:
2l2=p-l1=64-24=40 cm e dividendo tutto per 2 otteniamo…
l2=20 cm
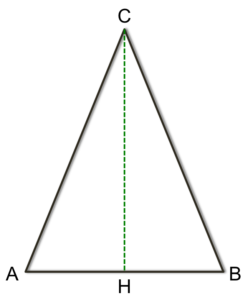
Abbiamo così trovato tutti i lati del triangolo isoscele. Possiamo calcolarne l’area utilizzando la formula di Erone oppure dividere il triangolo isoscele in due triangoli rettangoli semplicemente tracciando l’altezza. Ci calcoliamo l’area di ciascuno di questi due triangoli e poi moltiplichiamo per 2.
Applichiamo la formula del Teorema di Pitagora (la n2 vista sopra) e calcoliamo l’altezza come il cateto del triangolo rettangolo AHC. Dai dati in nostro possesso sappiamo che:
AC=20 cm
AB=24 cm → AH=AB/2=12 cm
C=√(i2-c2)=√(202-122)=√400-144=√256=16
CH=16 cm
L’area del triangolo rettangolo AHC è quindi bxh/2 cioè:
AAHC=(16×12)/2= 96 cm2
Moltiplichiamo per 2 per ottenere l’area totale ABC
AABC=96×2=192 cm2
Dimostrazione della formula del Teorema di Pitagora
Non esiste un’unica dimostrazione del Teorema di Pitagora, ma sono addirittura centinaia. Da quella di Perigal del 1873 a quella di Tempelhoff del 1769 o di Nassir del 1594 … alcune davvero si perdono nella storia. Noi ve ne proponiamo una semplice e creativa, proposta da James Garfield nel 1876 e dopo vi racconteremo anche un aneddoto interessante su come è arrivato a questa dimostrazione.
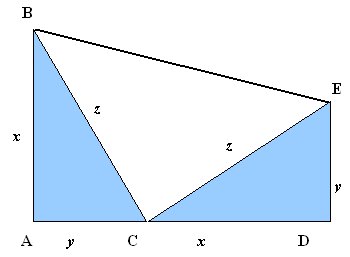
Osserviamo l’immagine (fonte Politecnico di Torino) e procediamo per step. In breve arriveremo a dimostrare il Teorema di Pitagora.
- Per prima cosa disegna su un foglio un triangolo rettangolo ABC di dimensioni generiche.
- Disegna un triangolo rettangolo isoscele partendo dall’ipotenusa BC. Il triangolo sarà BCE (quello bianco in figura). Quindi BC=EC
- Prolunga il lato AC fino a quando non incontri la perpendicolare che parte da E.
Analizziamo i triangoli ABC e CDE, notiamo che:
- il lato BC è uguale al lato EC (perché è un triangolo rettangolo isoscele, per cui i cateti sono uguali)
- l’angolo ECD=180°-BCE-BCA → ECD=180°-90°-BCA → ECD=90°-BCA (per differenza da un angolo piatto)
- l’angolo CED=180°-EDC-ECD → CED=180°-90°-(90°-BCA) → CED=BCA (perché la somma degli angoli di un triangolo è 180°)
- I lati opposti ad angoli opposti sono uguali per cui AB=CD (che in figura sono indicati con x)
- Ne consegue che CA=ED (che in figura sono indicati con y)
Abbiamo dimostrato che i triangoli azzurri sono uguali. Analizziamo la figura ABDE, si tratta di un trapezio rettangolo dove l’altezza è AD (x+y) e le basi sono AB (x) e DE (y).
L’area del trapezio rettangolo è A=(b+B)xh/2 → A=(x+y)(x+y)/2
L’area del trapezio può anche essere calcolata come somma dell’area del triangolo bianco più l’area dei due triangoli blu (che sono uguali), cioè: A=z2/2+2(xy)/2
Poniamo l’uguaglianza tra le due formule delle aree per trovare:
(x+y)(x+y)/2=z2/2+2(xy)/2
Moltiplichiamo tutto per 2 per ottenere:
(x+y)(x+y)=z2+2xy
Portiamo 2xy a sinistra e eseguiamo la moltiplicazione:
x2+y2+2xy-2xy=z2
x2+y2=z2
Abbiamo così ottenuto la dimostrazione della formula del teorema di Pitagora.
Curiosità sulla formula del Teorema di Pitagora
James A. Garfield fu il ventesimo presidente degli Stati Uniti. Fu eletto nel 1880 e sin da subito si dimostrò un convinto anti-schiavista, avviando una campagna contro la corruzione politica. Ciò gli causo l’astio di numerosi nemici e fu sparato con una pistola pochi mesi dopo essere stato eletto. Morì alcuni giorni dopo.
Egli riusci a trovare, in uno dei suoi momenti di svago, la brillante dimostrazione del teorema di Pitagora che presentò ai suoi colleghi del Congresso dicendo: “Pensiamo che con questa dimostrazione matematica possiamo trovare d’accordo tutti i deputati, indipendentemente dal loro credo politico”.