Tag: Figure Geometriche Piane

Quali sono le figure geometriche piane? Come riconoscerle e quali caratteristiche hanno? Qual è la differenza tra figure geometriche piane e solide?

In questa lezione vedremo una breve carrellata su tutte le figure piane che si studiano nella geometria delle scuole elementari, medie e nel biennio delle superiori. Per ciascuna di esse troverai degli approfondimenti da seguire con esercizi e parte teorica.

Cosa sono figure geometriche piane?

Il termine figura deriva dal latino e sta ad indicare la rappresentazione di una forma e delle dimensioni di un oggetto.

Le figure geometriche servono quindi a rappresentare in maniera più semplicistica gli oggetti che possiamo osservare tutti i giorni. Ad esempio lo schermo del monitor può essere approssimato ad un rettangolo, le mattonelle a quadrati o rettangoli, eccetera…

Definizione: le figure geometriche piane sono degli oggetti matematici bidimensionali formati da un insieme di punti.

Differenza tra figure geometriche piane e solide

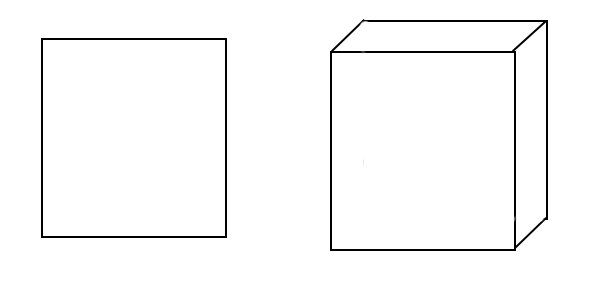
Nella definizione è comparso il termine “bidimensionale”. Tutta le figure piane appartengono ad un piano. Hanno una larghezza e un’altezza, ma non una profondità.

Esempio:

Prova a disegnare un triangolo su un foglio di carta. Potrai renderti conto che il triangolo appartiene interamente al foglio (cioè al piano su cui stai disegnando).

Le figure solide, invece, si materializzano anche nella terza dimensione. Cioè hanno larghezza, altezza e profondità.

Quali sono le figure piane della geometria?

Di seguito vediamo una carrellata completa delle principali figure geometriche piane partendo dall’ente semplice più elementare fino a quello più complesso. Ti basterà cliccare sul nome per aprire la lezione di approfondimento.

• il punto: alcuni testi lo definiscono come la traccia lasciata dal gesso sulla lavagna.
• il segmento: è un insieme di punti allineati delimitato da due estremi.
• la semiretta: è un insieme di punti allineati delimitato da un estremo.
• la retta: è un insieme infinito di punti allineati.

Assieme al piano questi sono i primi enti fondamentali che si studiano nella geometria piana. Si passa poi a studiare i poligoni, ovvero le figure piane formate da più angoli (e lati)

• Triangolo: sono dei poligoni formati da tre lati e tre angoli. In base ai rapporti e alle misure di questi si distinguono:
  • triangolo rettangolo
  • triangolo isoscele
  • triangolo equilatero
  • triangolo scaleno

• Quadrato: è un poligono regolare formato da 4 lati (e angoli) uguali tra loro.

• Rettangolo: è un quadrilatero formato da lati uguali e paralleli a due a due. Gli angoli invece sono tutti uguali.

• Parallelogramma: è un quadrilatero formato da lati uguali e paralleli a due a due. Anche gli angoli sono uguali a due a due.

• Trapezio: è un quadrilatero con due lati paralleli (basi) e due lati obliqui. A seconda delle dimensioni di questi ultimi possiamo distinguere:
  • Trapezio scaleno
  • Trapezio isoscele
  • Trapezio rettangolo

• Cerchio/Circonferenza: è l’insieme dei punti equidistanti da un punto fisso detto centro.

• Rombo: è un poligono regolare composto da 4 lati.  I lati sono paralleli a due a due.

• Pentagono: è un poligono composto da 5 lati (penta = 5)

• Esagono: è un poligono composto da 6 lati (esa=6)

• Ettagono: è un poligono composto da 7 lati (etta=7)

• Ottagono: è un poligono composto da 8 lati (ott=8)

• Ennagono: è un poligono composto da 9 lati (enn=9)

• Decagono: è un poligono composto da 10 lati (deca=10)

• Dodecagono: è un poligono composto da 12 lati (dodeca=12)

In basso trovi un elenco di tutte le lezioni e gli approfondimenti sulle figure geometriche piane. Clicca sulla lezione per scoprire teoria ed esercizi da svolgere.