Christian ci scrive: “Come si calcola l’area del triangolo equilatero? Quali sono le formule e le regole da utilizzare per svolgere gli esercizi?”
RISPOSTA
L’area di un triangolo equilatero è la superficie compresa all’interno dei 3 lati. E possibile calcolarla utilizzando formule più o meno semplici che vedremo all’interno di questo approfondimento.
Area del triangolo equilatero – le formule
La premessa è che valgono tutte le regole e le formule viste per calcolare l’area di un triangolo scaleno. Quindi la prima e più utilizzata da prendere in considerazione è base per altezza diviso due.
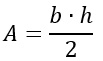
Visto che questa figura ha la particolarità di avere tutti i lati congruenti, la formula può essere riscritta in maniere differenti. Nella lezione sull’altezza del triangolo equilatero abbiamo già visto alcune formule che permettono di calcolare l’altezza partendo dal lato. Possiamo fare un discorso analogo con la superficie della figura.
Ecco le formule dirette da utilizzare:
Noto il lato
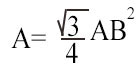
Nota l’altezza
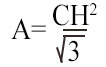
Noto il perimetro
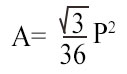
Dimostrazione della formula dell’area dato il lato
Per calcolare l’area del triangolo equilatero, dobbiamo sfruttare la formula generale valida per tutti i triangoli:
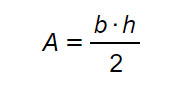
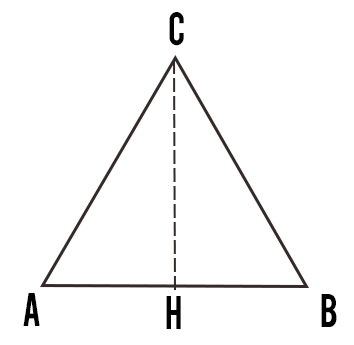
La base in questo caso è il lato del triangolo AB in figura. L’altezza invece è il segmento che parte da un vertice e cade perpendicolarmente sul lato opposto. Nel disegno in figura, h=CH. Per cui riscrivendo la formula dell’area del triangolo equilatero ho:
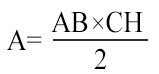
Conoscendo il lato AB=BC=CA, resta da determinare l’altezza CH. Questa può essere calcolata usando il teorema di Pitagora e considerando il triangolo rettangolo CHB. (triangolo di 30-60-90 gradi). Poiché l’altezza è anche mediana nei triangoli equilateri, allora possiamo scrivere che:
HB=CB:2 → HB=AB:2 poiché tutti i lati del triangolo sono uguali.
Usando la formula inversa del teorema di Pitagora ho:
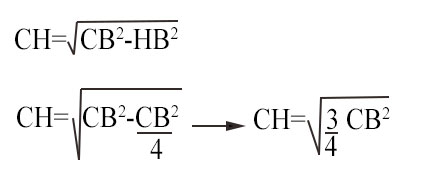
Eseguendo la radice quadrata si ottiene la formula risolutiva:
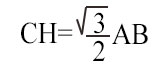
Calcolata quindi l’altezza, possiamo passare al calcolo dell’area del triangolo equilatero.
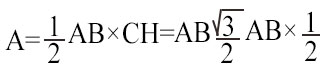
Semplicemente facendo un paio di moltiplicazioni si ottiene la formula finale:
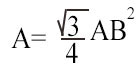
Area triangolo equilatero – esercizi svolti
Esercizio 1.
Calcolare l’area del triangolo equilatero che ha il lato che misura 10 cm.
Le possibili strade per ottenere la soluzione sono due. Nel primo metodo, quello più lungo:
- calcolare la metà del lato;
- applicare la formula inversa del teorema di Pitagora per ottenere l’altezza;
- calcolare l’area con la formula generale base per altezza diviso due.
Con il secondo metodo andiamo direttamente ad applicare la formula diretta vista in questa lezione. E’ noto un lato e bisogna calcolare l’area del triangolo equilatero. Per cui la formula da usare è:
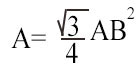
A=(√3):4×10=4,33 cm.
Esercizio 2.
Calcolare l’area del triangolo equilatero con l’altezza che misura 20 cm.
Il metodo più diretto per risolvere l’esercizio è sicuramente quello di utilizzare la formula vista in questa lezione.
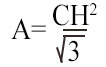
A=20²:(√3)=400×1,732=230,96 cm²

Un secondo metodo potrebbe essere quello di calcolare l’area del triangolo CHB di cui conosciamo il cateto maggiore CH. Si tratta, come già detto prima, di un triangolo rettangolo da 30-60-90.
- L’ipotenusa è il lato del triangolo equilatero;
- Il cateto minore è la metà del lato del triangolo equilatero;
- Il cateto maggiore è l’altezza del triangolo equilatero.
Quindi possiamo scrivere il teorema di Pitagora:
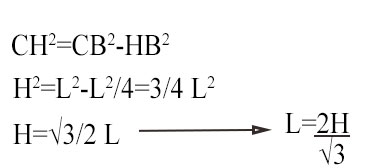
L=40/1,732=23,09 cm²
A questo punto posso calcolare l’area utilizzando la prima formula (area triangolo equilatero noto il lato)
A=230,96 cm²
Esercizio 3
Data l’area del triangolo equilatero, calcolare il perimetro. A=96cm².
Come abbiamo visto nella lezione sui perimetri dei triangoli, possiamo utilizzare la formula semplificata P=3L. Quindi è necessario calcolare il lato partendo dall’area. Dalla prima formula vista, ricaviamo la inversa per ottenere il lato.
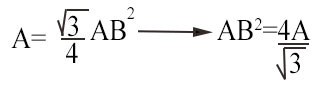
AB²=221,70 cm²
Per ottenere il risultato finale, è sufficiente fare una radice quadrata ad entrambi i membri.
AB=14,89 cm.
Approfondimenti: Area triangolo scaleno – quali formule usare?