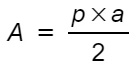I poligoni regolari sono delle particolari figure geometriche piane che hanno tutti gli angoli e i lati uguali. Sono qui poligoni equilateri ed equiangoli.
Nella lezione di oggi vedremo quali sono i poligoni regolari, come riconoscerli e quali proprietà hanno. Per ogni figura che incontrerai, troverai poi tanti approfondimenti con formule, teoria ed esercizi svolti.
Definizione
Come già detto ad inizio lezione, i poligoni regolari sono dei poligoni convessi con tutti i lati congruenti. Ciò implica che ogni poligono regolare ha tutti i lati e gli angoli uguali.
Si definiscono quindi poligoni irregolari, tutti gli altri che non sono né equilateri né equiangoli.
Classificazione dei poligoni regolari
A seconda del numero di lati, possiamo distinguere diverse figure e tutte rientrano nella categoria dei poligoni regolari. Ecco tutte le figure geometriche piane regolari che si studiano nelle scuole. Clicca sull’immagine per andare alla lezione di approfondimento per ogni singola figura.
Quadrato
Pentagono
Esagono
Ettagono
Ottagono
Ennagono
Decagono
Endecagono
Dodecagono
Tridecagono
Tetradecagono
Caratteristiche
- I poligoni regolari hanno sempre tutti i lati e gli angoli uguali.
- Ogni poligono regolare è sempre inscrivibile e circoscrivibile in una circonferenza.
Definizione di apotema
L’apotema è la misura del raggio della circonferenza inscritta nel poligono regolare. Su alcuni libri di testo si legge anche che l’apotema è il segmento che parte dal baricentro del poligono e cade perpendicolarmente sul lato opposto.
Numero fisso e costante d’area
Ogni figura ha due numeri che restano fissi indipendentemente dalle sue dimensioni. Vengono definite come numero fisso f e costante d’area φ.
Questi due costanti servono per mettere in relazione il lato con l’apotema (nel caso del numero fisso) e l’area (nel caso della costante d’area). Per cui, dato il lato L del generico poligono regolare, è sempre possibile trovare apotema ed area.
Formule poligoni regolari
Ci sono alcune formule che possono essere considerate generiche e valgono per tutte le figure geometriche equilateri ed equiangoli.
Perimetro di un poligono regolare
Il perimetro p si ottiene semplicemente moltiplicando la misura del lato L per il numero di lati N della figura.
p = N · L
Area di un poligono regolare
- Dato il lato: è sufficiente moltiplicare il lato al quadrato per la costante d’area. Per cui la formula è:
A = f · L²
- Dato apotema e perimetro: si moltiplica il semiperimetro per la misura dell’apotema. Per cui la formula è:
Combinando queste 3 formule ed utilizzandone le formule inverse, è possibile conoscere tutte le misure di un generico poligono regolare.