Le intersezioni con gli assi sono i punti di intersezione di una generica funzione f con gli assi cartesiani. Si tratta di un argomento estremamente importante nello studio di funzione perché permette di trovare preziosi informazioni sul grafico da disegnare.
Nel programma di geometria analitica avevamo già visto come trovare l’intersezione tra due rette. In questa lezione andremo a riprendere quanto già detto estendendo però il ragionamento a qualsiasi tipo di curva e funzione. Come si trovano i punti di intersezione con gli assi di una parabola, di una retta o di una qualsiasi funzione?
In questa lezione vedremo in maniera approfondita il calcolo delle intersezioni con gli assi cartesiani con degli esercizi sulle funzioni fratte, logaritmiche ed esponenziali. Per la comprensione di questa lezione è importante sapere come si risolvono i sistemi di equazioni.
Quali sono le intersezioni con gli assi?
I punti di intersezione del grafico con gli assi cartesiani sono dei punti che si ottengono intersecando la funzione y=f(x) con l’asse delle ascisse (che ha coordinate y=0) e con l’asse delle ordinate (che ha coordinate x=0).
Non è detto che la nostra funzione abbia dei punti di intersezione con gli assi, ma dalla loro individuazione si possono già ricavare preziose informazioni da riportare sul grafico. Vediamo come procedere con questo doppio calcolo in maniera semplice.
Intersezione con l’asse y (x=0)
E’ necessario costruire un sistema composto da due equazioni. Sul primo rigo avremo la funzione y=f(x), sul secondo rigo l’equazione dell’asse delle ordinate x=0.
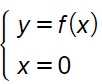
Questo significa, in parole povere, che bisogna trovare un punto che ha coordinate P(0 ; yP) dove yP = f(0) lo si determina andando a sostituire, all’interno della funzione, al posto della x il valore 0.
E’ in genere il calcolo più immediato che può essere risolto a volte addirittura a mente grazie alla sua semplicità. Vedrai negli esercizi svolti dopo quanto questo calcolo sia semplice.
ATTENZIONE: non è detto che esista l’intersezione con l’asse delle ordinate. Se questo punto esiste, sarà unico, in base alla definizione di funzione. Ricordi cosa avevamo detto? Che per ogni valore di x associa uno e un solo valore di y, per cui non possono esserci 2 intersezioni con l’asse delle y.
Intersezione con l’asse delle x (y=0)
E’ necessario costruire un sistema composto da due equazioni. Sul primo rigo avremo sempre la funzione y=f(x), mentre sul secondo rigo metteremo la retta corrispondente all’equazione dell’asse delle x, ovvero y=0.
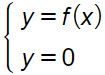
Il punto di intersezione con l’asse delle ascisse ha coordinate P(xP;0). Per trovare l’ascissa del punto di intersezione con gli assi bisogna quindi andare a sostituire il valore 0 al posto della y. Dalla risoluzione dell’equazione che si ottiene ci sono due possibili casi:
- le equazioni sono impossibili o non hanno soluzioni: non ci sono intersezioni con l’asse x;
- le equazioni ammettono 1 o più soluzioni: queste sono proprio i valori delle ascisse dei punti di intersezione con l’asse x.
Un primo semplice esempio
Proviamo subito a mettere in pratica quello che abbiamo scritto in termini generici con un facile esercizio svolto.
Calcolare le intersezioni con gli assi della funzione:
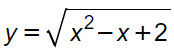
Intersezioni con l’asse delle ordinate
x=0
y=√(0²-0+2) → y=√2
Quindi abbiamo semplicemente sostituito, nell’equazione della funzione, il valore 0 al posto della x. Abbiamo così trovato il primo punto di intersezione con gli assi cartesiani: P(0; √2)
Intersezioni con l’asse delle ascisse
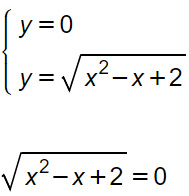
Come puoi vedere in questo caso, andando a sostituire al posto della y il valore 0 nella funzione, si ottiene un’equazione irrazionale. Quini dobbiamo determinare le condizioni di esistenza e poi elevare al quadrato. In realtà, quando effettueremo lo studio di funzione completo, le condizioni di esistenza non saranno necessarie perché non saranno altro che una ripetizione del dominio della funzione.
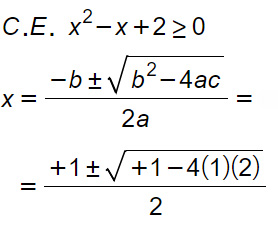
La disequazione di secondo grado, una volta risolta, mi dà come risultato un delta negativo. Questo vuol dire che non ci sono intersezioni con l’asse delle ordinate.
Intersezioni con gli assi di una funzione logaritmica
Calcolare le intersezioni con gli assi cartesiani della funzione:
y=log(x-1)
In questo caso abbiamo una funzione logaritmica da studiare. Il procedimento è sempre lo stesso per cui iniziamo subito con i calcoli.
ATTENZIONE: quando andrai a studiare la funzione negli esercizi di analisi, dovrai per prima cosa calcolarne il dominio. In questo caso la condizione di esistenza della funzione è x-1>0, cioè x>1. Questo significa che è inutile calcolare l’intersezione con l’asse y (cioè mettere a sistema con x=0) perché i valori delle x validi sono da +1 fino a infinito. Non sei convinto? Proviamo a calcolare comunque l’intersezione con l’asse delle ordinate
Intersezione con l’asse y
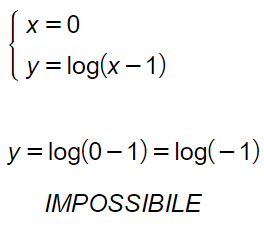
Come puoi vedere il calcolo non ha fatto altro che confermare quello che già dal dominio potevamo intuire. Per cui, per evitare di sprecare tempo e fare calcoli inutili, fai attenzione al dominio prima di trovare le intersezioni con gli assi.
Intersezione con l’asse x
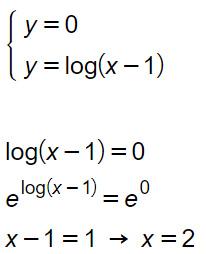
Una volta imposto il sistema, abbiamo semplicemente risolto l’equazione logaritmica che ne è derivata e siamo arrivati alla soluzione.
P(2;0)
Intersezioni con gli assi delle funzioni esponenziali
Trovare i punti di intersezione con gli assi cartesiani della funzione:

Intersezione con l’asse x
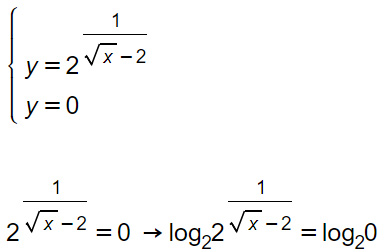
L’intersezione con l’asse x non porta ad alcun risultato perché il logaritmo di 0 non esiste nel campo dei numeri reali. Per cui la funzione non si interseca con l’asse delle ascisse.
Intersezione con l’asse y
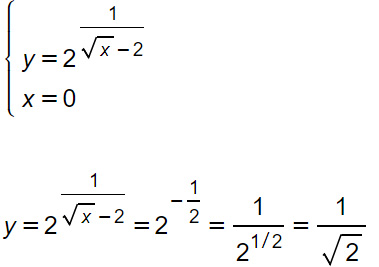
L’esercizio potrebbe anche essere terminato ma vogliamo esprimere più correttamente il valore dell’ordinata, per cui è necessario eseguire una razionalizzazione del radicale.
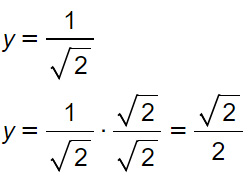
Conclusioni
Abbiamo visto come il calcolo delle intersezioni con gli assi della generica funzione si risolve imponendo un sistema di due equazioni in due incognite. Dalla risoluzione del sistema si ottengono le coordinate dei punti che appartengono sia alla funzione che agli assi cartesiani.
Se la lezione ti è stata utile, l’hai trovata chiara o se hai ancora dei dubbi, lascia un commento qui in basso. Il nostro staff ti risponderà nel minor tempo possibile.