Categoria: La parabola in matematica nel piano cartesiano

Una lezione riepilogativa sulla parabola nel piano cartesiano. Troverai in questa scheda, un sunto di tutto quello che bisogna sapere con vari approfondimenti da consultare.

Partendo dalla definizione, vedremo le formule della parabola nei vari casi, le equazioni da studiare, i casi di tangenza con le rette ed alcuni interessanti esercizi svolti.

Definizione di parabola

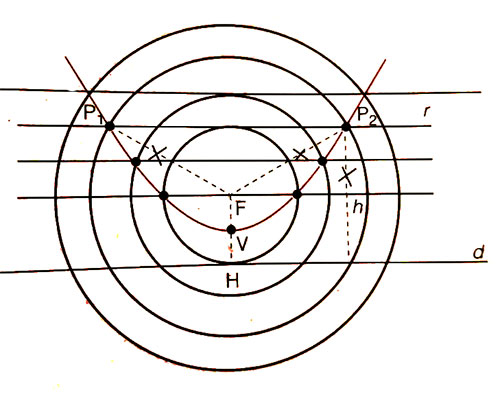
La parabola in matematica è il luogo dei punti del piano equidistanti da un punto fisso F, detto fuoco e da una retta fissa detta d, detta direttrice.

Il punto medio V del segmento FH, perpendicolare alla direttrice, appartiene alla parabola e viene detto vertice della parabola.

Infine l’asse di simmetria è quella retta che divide in due parti uguali la figura. Nel disegno in basso è una retta verticale.

Formule parabola

In questa lezione riepilogativa non ci dilungheremo molto sulle dimostrazioni o nelle spiegazioni, ma illustreremo solo una tabella completa con tutte le formule della parabola.

Per approfondimenti ti rimandiamo alla lezione sull’equazione della parabola.

Formule della parabola con asse parallelo all’asse y

y=ax²+bx+c

Si tratta di un’equazione di secondo grado a due incognite, x e y. a, b e c invece sono i tre coefficienti numerici che individuano la posizione esatta della figura nel piano cartesiano.

a> 0 → concavità verso l’alto

a<0 → concavità verso il basso

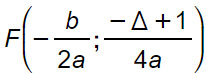
Fuoco

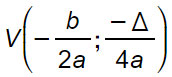
Vertice

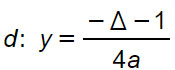
Direttrice

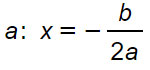
Asse

Formule parabola con asse parallelo all’asse x

x=ay²+by+c

Per passare dall’equazione della parabola ad asse verticale ad asse orizzontale, basta sostituire la x con la y.

a>0 → concavità rivolta verso destra

a<0 → concavità rivolta verso sinistra

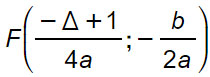
Fuoco

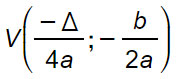
Vertice

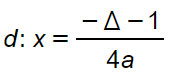
Direttrice

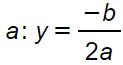
Asse

Come disegnare una parabola

Per rappresentare graficamente una parabola di equazione y=ax²+bx+c, conviene, dopo aver esaminato se rivolge la concavità verso il basso o verso l’alto, determinare il vertice, l’asse, l’intersezione con l’asse y, le eventuali intersezioni con l’asse x e se è il caso altri suoi punti, tenendo conto che essa è simmetrica rispetto al suo asse.

Il nostro consiglio è di calcolare subito il vertice e un punto appartenente alla parabola. A quel punto se ne calcola il simmetrico. Si otterranno così 3 punti per i quali passa una ed una sola parabola.

Esempio

y=2x²-5x-3

Svolgimento

La parabola ha equazione con asse di simmetria verticale e, poiché a=2>0, la concavità è rivolta verso l’alto. Calcoliamo quindi il vertice.

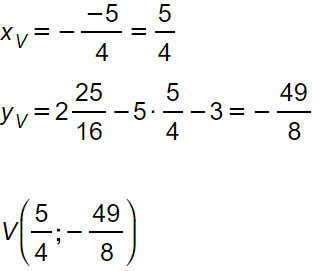
A questo punto, assegno un valore arbitrario alla x e lo sostituisco nell’equazione della parabola. Per renderci la vita più semplice sostituiamo x=0, che corrisponde all’intersezione con l’asse y.

y=2(0)²-5(0)-3 → y=-3
P(0;-3)

Disegno i due punti sulla parabola e individuo graficamente il simmetrico di P. E’ sufficiente unire i tre punti per rappresentare la parabola. Lasciamo a te quest’ultima parte del disegno.

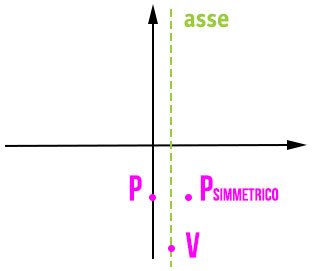
Di seguito trovi tutti gli approfondimenti e le lezioni sulla parabola. Troverai alla fine di ogni argomento un’abbondante parte dedicata agli esercizi svolti.