Categoria: Rombo
Il rombo è una figura geometrica con quattro lati congruenti. E’ un poligono regolare convesso che ha quindi tutti i lati uguali e quelli opposti sono paralleli tra loro.
In questa lezione vedremo quali sono le principali formule del rombo geometrico, così da avere sempre a disposizione un comodo formulario da usare nello svolgimento degli esercizi.
Analizzeremo nella prima parte alcuni concetti teorici, quindi caratteristiche, proprietà e definizione di rombo, per poi vedere alcuni esercizi e problemi svolti.
Definizione di rombo
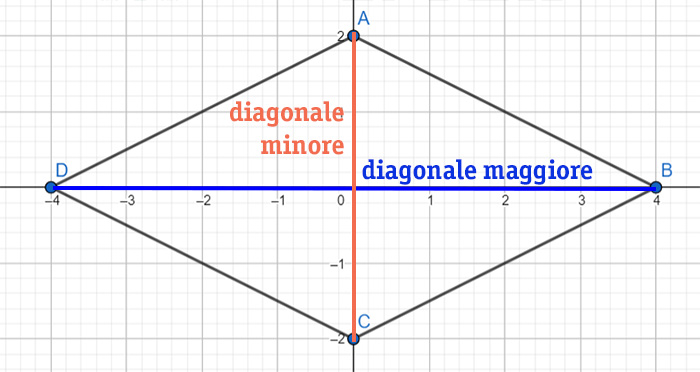
Il rombo è un quadrilatero con tutti i lati uguali e gli angoli opposti uguali.
Prima di analizzare le formule del rombo vediamo che cos’è e che caratteristiche ha questa figura.
- ha 4 lati congruenti proprio come il quadrato
- ha due diagonali
- gli angoli opposti sono congruenti
- i lati opposti sono paralleli
- ha una diagonale maggiore e una diagonale minore
- le due diagonali sono tra loro perpendicolari
Formule rombo
Ecco un formulario completo con tutte le formule principali che possono essere utilizzate negli esercizi.
Perimetro del rombo
![]()
Per il calcolo del perimetro del rombo bisogna moltiplicare per 4 la misura del lato.
Area del rombo
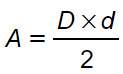
Come si trova l’area del rombo? Questa è uguale al semi-prodotto delle due diagonali. Cioè si calcola facendo diagonale maggiore per diagonale minore diviso due.
In pratica per calcolare l’area di un rombo basta considerare che le sue diagonali lo dividono in quattro triangoli rettangoli.
Rombo formule inverse
Dalle prime due formule viste è facile ricavare le formule inverse del rombo. Queste ci permettono di calcolare le due diagonali e il lato a partire dalla misura dell’area e del perimetro.
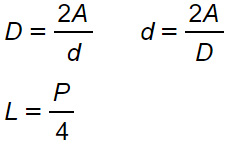
Rombo formule secondarie
Di seguito elenchiamo le formule “secondarie”, cioè un insieme di formule ricavate attraverso pochi passaggi algebrici. In genere non consigliamo di impararle a memoria, ma suggeriamo ai nostri studenti di capire come sono state ricavate.
Lato con le diagonali
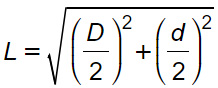
Sfruttando il teorema di Pitagora, il lato del rombo si calcola considerando le semi diagonali come cateti e il lato come ipotenusa.
Formule rombo e circonferenza inscritta (con dimostrazione)
Il rombo può sempre essere inscritto in una circonferenza di raggio r.
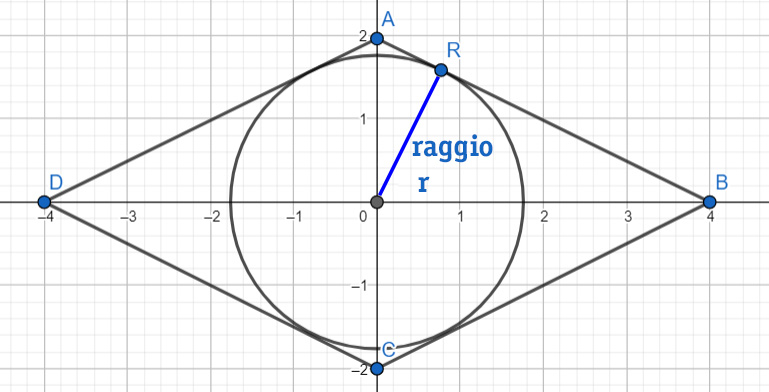
Dal disegno notiamo che il triangolo AOB è rettangolo e il raggio r è l’altezza perpendicolare alla base AB. Usando la formula dell’area dei triangoli A=bxh:2, possiamo scrivere che l’area in funzione del raggio della circonferenza inscritta.
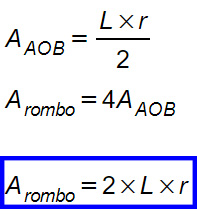
Formula inversa
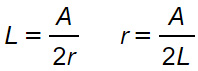
Per calcolare il lato basta dividere l’area per la misura del diametro della circonferenza inscritta.
Allo stesso modo il raggio della circonferenza inscritta si calcola dividendo l’area per il doppio del lato.