Abbiamo già parlato nelle precedenti lezioni delle proprietà del triangolo equilatero. Oggi vedremo un approfondimento più specifico: che cosa succede quando abbiamo un triangolo equilatero inscritto in una circonferenza?
Quali formule bisogna utilizzare e come si risolvono i problemi? A tutte queste domande risponderemo analizzando diversi casi ed esercizi svolti. Iniziamo però subito capendo quando un triangolo equilatero è inscritto all’interno di una circonferenza.
Definizione
Un triangolo equilatero si definisce inscritto in una circonferenza quando le due figure hanno solo 3 punti in comune.
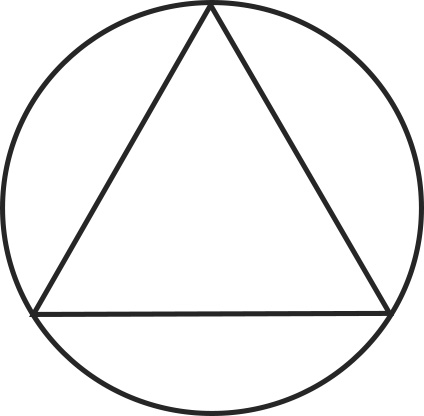
Come puoi osservare dalla figura i tre vertici del triangolo toccano la circonferenza. Si può anche dire infatti che la circonferenza è circoscritta al triangolo.
Formule da usare
Ne vedremo la dimostrazione tra pochissimo. Iniziamo dicendo subito che è sufficiente avere il raggio per conoscere il lato del triangolo.
l=r√3
dove l è la misura del lato del triangolo equilatero, mentre r è il raggio della circonferenza circoscritta.
Da questa possiamo ricavare la formula inversa che permette di trovare il raggio a partire dal lato del triangolo.
r=l / √3
Dimostrazione e proprietà
Indicando con C il centro della circonferenza, proviamo ad unire questo con i vertici del triangolo.
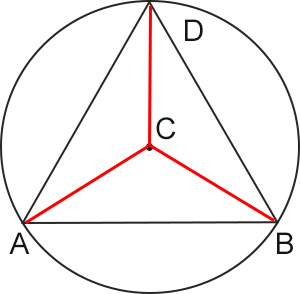
Puoi notare che si formano tre triangoli isosceli: ACD, ABC, BCD. A questo punto per ogni triangolo isoscele possiamo disegnare l’altezza (che sappiamo anche essere mediana e bisettrice).
Considerando che si formano 3 angoli perfettamente uguali, allora gli angoli che partono dal punto C sono tutti di 120° (essendo 360° diviso il numero di angoli che si formano, cioè 3, allora ognuno sarà di 120°).
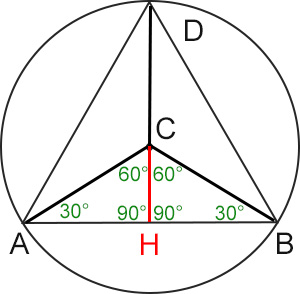
Prendiamo ad esempio il triangolo ABC. Tracciano l’altezza CH si formano due triangoli rettangoli congruenti: ACH e HCB. Sappiamo che:
- AC = CB = raggio della circonferenza = r
- L’angolo ACB = 120°, per cui ACH=HCB=60°
I due triangoli AHC e CHB sono triangoli rettangoli da 30°, 60° 90°. Questo significa che CH = AC/2 = r/2
Applicando il teorema di Pitagora, possiamo ricavare AH.
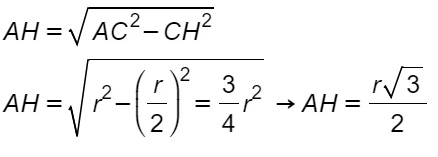
Poiché AH è metà base del triangolo equilatero, allora il lato di quest’ultimo è pari a:
AB=AD=DB → l=r√3
Abbiamo quindi capito che quando nel triangolo equilatero inscritto alla circonferenza è sufficiente avere il raggio, per poter così conoscere le misure di tutti i lati.
Esercizio svolto
Un triangolo equilatero ABC è inscritto in una circonferenza che misura 100π. Calcolare l’area del triangolo equilatero, l’area del cerchio, l’area della parte di cerchio colorata.
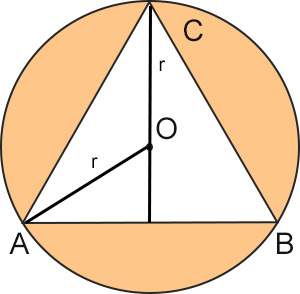
Svolgimento
Ricordi le formule di cerchio e circonferenza? Nota la lunghezza della circonferenza posso calcolare il raggio:
C=2πr → r=C/2π
r=100π/2π = 50 cm
Usiamo la formula che abbiamo dimostrato che ci permette di trovare il lato del triangolo dato il raggio.
l = r√3 = 50√3
A questo punto calcoliamo l’altezza CH con la formula inversa del teorema di Pitagora.
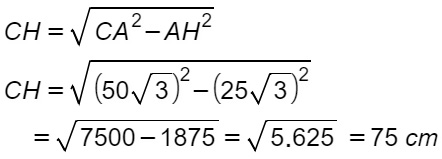
A questo punto possiamo calcolare l’area del triangolo con la formula generale base per altezza diviso due.
At = 50√3 · 75 = 6.495 cm²
Possiamo poi calcolare l’area del cerchio come pigreco per raggio alla seconda, così da ottenere:
Ac = π·50²= 7.850 cm²
Per calcolare infine l’area colorata della figura basta eseguire la sottrazione tra area più grande del cerchio e quella più piccola del triangolo.
A = 7.850 – 6.495 = 1.355 cm².