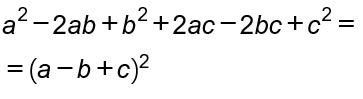Categoria: Scomposizioni di polinomi

La scomposizione di polinomi, chiamata su alcuni libri di matematica “fattorizzazione”, consente di scomporre un qualsiasi polinomio nel prodotto di più fattori.

La scomposizione in fattori di polinomi è importantissima per imparare a risolvere esercizi ed espressioni di algebra in cui il grado del polinomio sia maggiore di uno.

Se in classe hai studiato l’argomento e la spiegazione non è stata molto chiara o se hai un test o un compito e non ti senti sicuro, in questa pagina trovi elencante tutti principali metodi di scomposizione dei polinomi. Iniziamo da quello più semplice.

Raccoglimento a fattore comune

Si basa sul fatto che all’interno del polinomio ci sia un monomio comune a tutti (cioè un massimo comune divisore). Questa tecnica di scomposizione di polinomi viene anche indicata con il termine “messa in evidenza”.

Si dice che si può mettere in evidenza qualcosa che hanno in comune i vari elementi che si sommano algebricamente in un polinomio. Cerchiamo di essere più precisi e chiari.

Messa in evidenza totale

Si calcola il M.C.D. tra i tutti i monomi all’interno del polinomio. Lo si mette fuori da una parentesi tonda e all’interno di quest’ultima si inseriscono nuovamente gli stessi monomi, divisi però per il MDC.

Vediamo un esempio pratico. Immaginiamo di avere il polinomio:

Il termine in comune (cioè il massimo comune divisore) è x. Per cui mettiamo la x fuori da una parentesi tonda.

=x (…)  –> Dividiamo a questo punto ciascuno dei tre monomi per il MDC e li riscriviamo all’interno della parentesi.

Messa in evidenza parziale

In questo caso la scomposizione del polinomio è parziale, cioè si effettua due volte e su elementi differenti. Vediamo un esempio pratico.

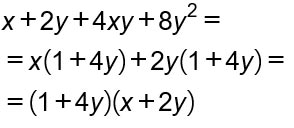
Sfoglia la lezione completa sul raccoglimento a fattor comune

Differenza di quadrati

E’ una delle scomposizioni di polinomi più semplici. Si applica tra due termini entrambi al quadrato e che hanno segni opposti.

Per risolvere è sufficiente riscrivere i monomi una volta utilizzando il segno positivo e una volta il segno negativo, come nell’esempio che segue.

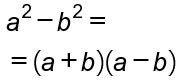
Vai alla lezione sulla differenza di quadrati

Differenza di cubi

Ricorre in molti esercizi e test, ma in pochi ricordano questo metodo di scomposizione di polinomi. Abbiamo due monomi al cubo separati da un segno meno. Ecco la regola generale.

Si riscrivono i monomi in una prima parentesi eliminando le potenze. Nella seconda parentesi si inseriscono i due monomi al quadrato e il loro prodotto, tutti e tre con il segno “più”.

Vai alla lezione sulla differenza di cubi

Somma di cubi

Metodo di scomposizione di polinomi molto simile alla precedente, ma questa volta abbiamo un segno più tra i due monomi di terzo grado.

Come prima: si mette una parentesi tonda con i due monomi senza le potenze. Nella seconda parentesi si inseriscono i due monomi al quadrato e il loro prodotto con il segno meno.

Vai alla lezione sulla somma di cubi

Scomposizione di polinomi (trinomio) di secondo grado

Si sfrutta la regola delle equazioni di secondo grado al contrario. E’ sufficiente riconoscere due termini al quadrato e il loro doppio prodotto. Ecco un semplice esempio:

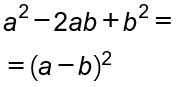
Si può risolvere anche con il metodo del trinomio speciale (o trinomio caratteristico) utilizzando la tecnica della somma e prodotto.

Vai alla lezione sul trinomio caratteristico

Quadrato di trinomi (6 termini)

Ti ricordi la regola per risolvere un quadrato di trinomio? Noi faremo il contrario, cioè partiamo da 6 termini per ottenerne 3 elevati al quadrato. Per applicare la scomposizione del polinomio, individua 3 termini che possono essere considerati dei quadrati e 3 doppi prodotti.

Troverai diversi esercizi sulle scomposizioni in cui applicare questa regole, per cui eccoti un semplice esempio.

Scomposizione polinomi – tutte le tecniche approfondite