Le proprietà dei logaritmi sono delle regole che permettono di svolgere le quattro operazioni applicate ai logaritmi. In questa lezione ne vedremo una spiegazione completa con alcuni facili esercizi per risolvere ogni dubbio o problema.
Prima di leggere questa lezione è importante che tu abbia già un’idea su cosa sia il logaritmo e quale sia il rapporto con gli esponenziali. Puoi dare un’occhiata alla nostra lezione di approfondimento sulla definizione di logaritmo.
Proprietà Logaritmi Tabella
![]()
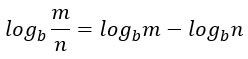
![]()
Prima di affrontare nel dettaglio le varie regole dei logaritmi riassunte in questa tabella, è importante saper riconoscere che cos’è la base e che cos’è l’argomento di questo particolare operatore matematico. Per questa ragione vediamo una spiegazione in breve sulla definizione di logaritmo.
Definizione di logaritmi
L’argomento di oggi è uno dei più odiati dagli studianti, che trovano le proprietà dei logaritmi difficili e vanno spesso in confusione con le varie regole. Iniziamo dando una facile definizione di logaritmi.
Che cosa sono i logaritmi? Per capirlo partiamo dall’equazione esponenziale più semplice. Per calcolare l’incognita in questa semplice equazione si passa al logaritmo di n in base b.
![]()
Per memorizzare questa regola puoi ricordarti che la base dell’esponente diventa la base del logaritmo. Ne deriva la seguente definizione di logaritmo:
Dicesi logaritmo di un numero positivo n, rispetto ad una base b, il numero x che si deve dare come esponente alla base b per ottenere un numero n.
Da questa spiegazione ricaviamo subito alcune proprietà dei logaritmi:
- Esistono solo logaritmi di numeri positivi.
- Il logaritmo di 1 fa 0. Questo perché l’esponenziale con indice di potenza 0 dà come risultato 1.
- Logaritmo di 0 è impossibile
- Il logaritmo della base logaritmica è 1. Detto in parole povere quando ho un logaritmo con base ed argomento uguali posso scrivere direttamente 1.
- Il logaritmo della base elevata ad un certo esponenziale è uguale a quell’esponente. Una spiegazione più semplice? Quando ho logaritmo con base ed argomento uguale con un esponente, il risultato è proprio pari all’esponente.
- Logaritmo di infinito vale infinito
Il logaritmo in base e
Viene comunemente chiamato logaritmo naturale il logaritmo che ha come base il numero di Nepero “e”. Non spaventarti quando lo incontri, segue tutte le regole dei logaritmi proprio come se fosse un normalissimo numero naturale. Troverai su molti libri di testo il logaritmo naturale indicato come ln.
Il logaritmo in base 10
E’ un logaritmo che si ritrova spesso sugli esercizi. Non ha nessuna differenza rispetto ai normali logaritmi se non per il fatto che ha base 10. Molto spesso sui libri di testo viene indicato con la dicitura Log, con la prima lettera maiuscola.
Regole e proprietà dei logaritmi
Le 4 regole che stiamo per analizzare saranno fondamentali non solo per risolvere i più facili esercizi sui logaritmi, ma anche per le equazioni logaritmiche che vedremo nelle prossime lezioni.
Prodotto e somma di Logaritmi
Il logaritmo di un prodotto è uguale alla somma dei logaritmi dei fattori.
![]()
Il prodotto di logaritmi, o meglio la moltiplicazione tra gli argomenti, si risolve scrivendo una somma di logaritmi con la stessa base.
Abbiamo già trattato l’argomento in maniera più approfondita nella lezione sulla somma di logaritmi. Per la dimostrazione della proprietà dei logaritmi, scriviamone due generici e applichiamo subito la definizione:
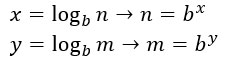
Applicando a questo punto la prima proprietà delle potenze possiamo ottenere:
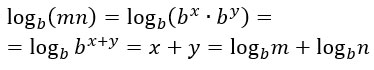
Divisione e differenza di logaritmi
Il logaritmo di un quoziente è uguale alla differenza tra il logaritmo del dividendo ed il logaritmo del divisore.
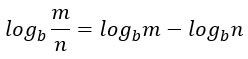
Per dimostrare questa proprietà dei logaritmi si applicano le stesse regole viste nella precedente dimostrazione. Posso quindi scrivere:
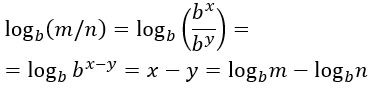
Vai all’articolo di approfondimento sulla differenza di logaritmi.
Potenza di un logaritmo
Il logaritmo di una potenza è uguale al prodotto dell’esponente per il logaritmo della base.
![]()
Questo significa che ogni volta che incontri una potenza, devi semplicemente portare fuori l’esponente dal logaritmo. Per la dimostrazione di questa proprietà dei logaritmi consideriamo:
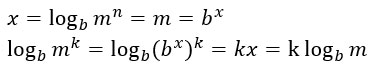
Questa regola può essere estesa anche alla radice di un logaritmo. Infatti la radice non è altro che una potenza dove l’indice di radice è il denominatore dell’esponente. Se non ricordi questa definizione, rileggi la lezione sulle regole dei radicali. Per cui possiamo scrivere:
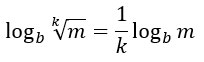
Esempio pratico: come si risolve il logaritmo al quadrato?
Esercizi facili sui logaritmi
In questa prima lezione proveremo a risolvere solo esercizi più facili mentre rimanderemo quelli più difficili ad una esercitazione interamente dedicata all’argomento.
Applica le proprietà dei logaritmi per risolvere le seguenti espressioni algebriche.
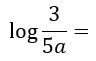
Notiamo che l’argomento del logaritmo presenta una divisione, per cui possiamo applicare la seconda proprietà dei logaritmi, quella relativa al rapporto.
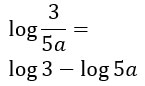
Esercizio 2
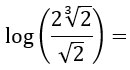
In questo secondo esempio sui logaritmi vediamo che ci sono diverse regole da applicare. Ci sono le radici, le potenze e le frazioni. Ecco come procedere:
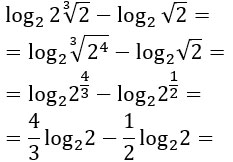
Abbiamo quindi prima applicato la seconda proprietà dei logaritmi, il rapporto, risolvendo così la frazione. Successivamente, applicando le regole dei radicali, abbiamo portato tutti i numeri sotto radice per applicare così la regola delle potenze dei logaritmi.
A questo punto è sufficiente fare un raccoglimento a fattor comune e poi calcolare il minimo comune multiplo tra le due frazioni.
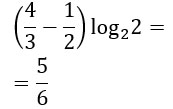
A questo link puoi trovare altri esercizi svolti sulle regole dei logaritmi. Per chiarimenti o per un aiuto a risolvere i tuoi esercizi sui logaritmi, contattaci! Il nostro staff è sempre a tua disposizione.
Grazie!