Ci scrive un nostro studente: Come si risolve un logaritmo al quadrato? Sto risolvendo un’equazione logaritmica e mi ritrovo logx^2, come posso procedere? Quale regola devo seguire? Grazie.
RISPOSTA
Il quadrato del logaritmo si risolve in maniera estremamente semplice andando a riprendere una delle proprietà dei logaritmi. In particolare possiamo ricordare che vale:
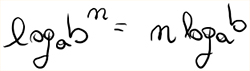
Quando cioè abbiamo il logaritmo con potenze, semplicemente l’esponente si sposta a sinistra del logaritmo, diventandone il coefficiente.
Come si risolve il logaritmo al quadrato?
In base alla regola che abbiamo appena visto, è facile rispondere al quesito posto dal nostro studente.
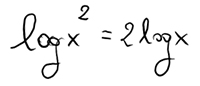
Possiamo quindi scrivere che logx^2 = 2 logx.
Elevamento al quadrato di un logaritmo generico
In questo caso il logaritmo ha base naturale (cioè base “e”, dove “e” è il Numero di Nepero). Come si calcola il quadrato del logaritmo quando c’è una base qualsiasi?
Non cambia assolutamente nulla. Ecco come procedere:
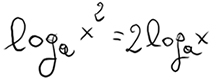
Esercizio
Proviamo a risolvere una piccola equazione logaritmica in cui compaia proprio il quadrato del logaritmo.
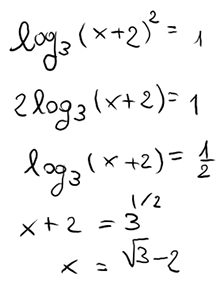
Subito dopo la traccia abbiamo applicato le regole dei logaritmi e spostato il quadrato del logaritmo facendolo diventare un coefficiente. Abbiamo diviso poi entrambi i membri per 2 e risolto l’equazione logaritmica trasformando il secondo membro in esponenziale, dove il risultato è 3 elevato a 1/2.
Ti ricordi le proprietà delle potenze? Quando un numero è elevato ad una frazione, il denominatore è l’indice di radice. Cioè 3 elevato a 1/2 diventa radice di 3.