Logaritmo di infinito – Quanto vale ln di infinito?

Uno dei nostri lettori ci pone il seguente quesito: quanto vale il logaritmo di infinito? Svolgendo un esercizio, devo calcolare il logaritmo naturale di infinito, cioè ln∞. Potete aiutarmi? Grazie

Una doverosa premessa prima di calcolare ln di infinito

Per evitare brutte figure durante un’interrogazione, è importante fare una piccola premessa. Chiedere quanto vale il logaritmo naturale di infinito potrebbe essere una domanda a trabocchetto. Questo perché è impossibile dare il risultato preciso sul comportamento di una funzione (come la funzione logaritmo) ad infinito. Non si può dare un risultato a ln(+∞) e ln(-∞).

Proprio per questa ragione si studia la teoria dei limiti e dell’intorno di un punto. Senza scendere troppo nei dettagli e per arrivare subito al punto, ti basti ricordare che in questi casi si va a studiare il comportamento della funzione negli intorni di infinito (nell’ipotesi che sia definita in un intervallo con l’infinito).

Quanto vale il logaritmo di infinito?

Cerchiamo subito di dare una risposta al nostro lettore a questo punto. La prima osservazione che facciamo è: di quale logaritmo stiamo parlando? La funzione generica logaritmo è:

y=log_ax

Ricordi quello che hai imparato quando hai studiato le proprietà dei logaritmi? La base “a” che può essere:

• maggiore di 1
• compresa da o e 1

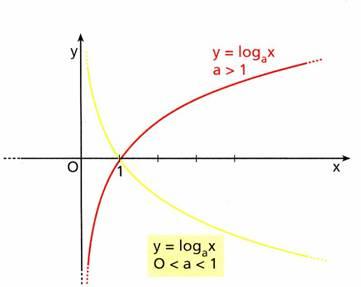
Anche il grafico della funzione cambia a seconda della base e di conseguenza anche il risultato della tua domanda (quanto vale il logaritmo di infinito). Analizziamo il comportamento delle due curve: la rossa e la gialla.

Logaritmo di infinito con base maggiore di 1

La curva rossa indica l’andamento della funzione logaritmo generica con base maggiore di 1. Che cosa succede quando la x va verso infinito? Detto in parole povere, la curva rossa dove tende man mano che si sposta verso destra? Verso l’alto… Cioè la sua y tende ad infinito. Per questa ragione ha senso dire che il logaritmo di infinito in questo caso vale infinito.

Logaritmo di infinito con base compresa tra 0 e 1

Facciamo lo stesso tipo di ragionamento per curva gialla. Quindi cosa succede quando questa si sposta verso destra. In altre parole cosa succede alla y quando la x si sposta verso destra? Che va verso il basso… Cioè la y tende a meno infinito. Per questa ragione possiamo dire che il logaritmo di infinito in questo caso vale meno infinito.

Conclusioni

Fermo restando quanto detto nella premessa, possiamo impropriamente dire che:

• il logaritmo di infinito con base maggiore di uno vale infinito → lim_x→+∞log_ax=+∞ , con a>1
• il logaritmo di infinito con base compresa tra zero e 1 vale meno infinito → lim_x→+∞log_ax=-∞ , con 0<a<1

Il risultato è esprimibile anche attraverso l’uso dei logaritmi, ma come hai potuto vedere sopra, è sufficiente ricordarsi semplicemente il grafico della funzione logaritmo per dare una risposta esauriente e corretta, così come abbiamo fatto quando abbiamo visto quanto vale il logaritmo di zero.