Il raccoglimento a fattor comune è la prima, la più semplice, ma anche la più ricorrente tecnica da usare per la scomposizione dei polinomi. In questa lezione vedremo la messa in evidenza totale e parziale di un polinomio.
Definizione
Raccoglimento a fattor comune totale
Raccoglimento a fattor comune parziale
Esercizi
Definizione di raccoglimento a fattor comune
Negli esercizi sui polinomi, che ti trovi spesso a dover affrontare nei compiti in classe o nelle verifiche, ci sono spesso delle operazioni che possono semplificarti notevolmente i calcoli. Si tratta delle scomposizioni di polinomi, cioè quelle operazioni che ti permettono di scomporre il polinomio in fattori, cioè in tanti elementi che si moltiplicano tra di loro.
Il raccoglimento a fattor comune, detto anche messa in evidenza, è la prima di queste tecniche e puoi utilizzarla nel momento in cui ti accorgi che ci sono degli elementi comuni che compaiono nei vari monomi. Può essere un numero, una radice o anche delle lettere.

Raccoglimento a fattor comune – il termine che si ripete sempre è proprio la x
Come si fa il raccoglimento a fattor comune totale?
Il tuo professore ti avrà certamente suggerito di applicare la proprietà distributiva, raccogliere i fattori e scrivere il polinomio dato come prodotto dei fattori comuni per un polinomio … E’ probabile che tu ci abbia capito poco, in realtà è molto più facile di quello che pensi.
Dal punto di vista didattico per fare il raccoglimento a fattor comune totale è necessario fare il massimo comune divisore (MCD) tra tutti gli elementi del polinomio e scrivercelo da parte. Un occhio un po’ allenato riesce a farne a meno e può capire al volo quali sono gli elementi che si ripetono nell’espressione che stiamo analizzando.
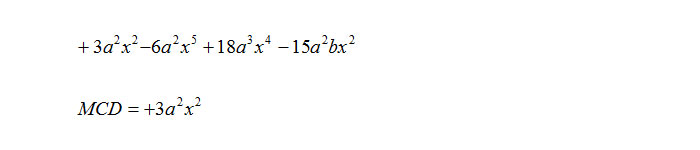
La prima operazione che abbiamo svolto nell’esempio è il massimo comune divisore. Abbiamo preso i fattori comuni presi una sola volta col minimo esponente per ottenere così un elemento che, guardando bene accomuna tutti i monomi. A questo punto si scrive l’elemento così individuato e si apre una parentesi tonda.
Si tratta a questo punto di fare la divisione di un polinomio per un monomio. Dentro la parentesi andranno gli elementi che si ottengono cioè dalla divisione tra monomi: quello di partenza il MCD.
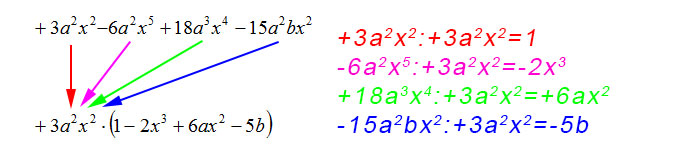
Ogni freccia corrisponde ad una divisione. Sulla destra trovi le operazioni svolte
L’esempio che abbiamo appena visto riguarda la messa in evidenza totale, o raccoglimento a fattor comune totale, dato che vengono coinvolti nel processo tutti gli elementi del polinomio.
Raccoglimento a fattor comune parziale
Il raccoglimento parziale può essere necessario quando non ci sono fattori comuni a tutti i termini del polinomio, ma solo ad alcuni. Generalmente è possibile fare il raccoglimento parziale tra gruppi di due o più polinomi. Vediamo nel dettaglio come procedere:

Raccogliendo a tra i primi due monomi e b tra i secondi due si ottiene un risultato particolare. Perché particolare? Perché a questo punto posso fare un raccoglimento a fattor comune totale nel nuovo polinomio individuato, dato che la parentesi (x+y) compare in ogni elemento dell’espressione.

Il raccoglimento a fattor comune parziale è un po’ più difficile proprio perché prevede due raccoglimenti da fare in due momenti diversi: il primo iniziale e parziale relativo solo a gruppi di monomi, il secondo totale in base al risultato ottenuto.
Esercizi sul raccoglimento a fattor comune
I primi esercizi sulla messa in evidenza che vi proponiamo sono già svolti, quindi hanno già la soluzione.
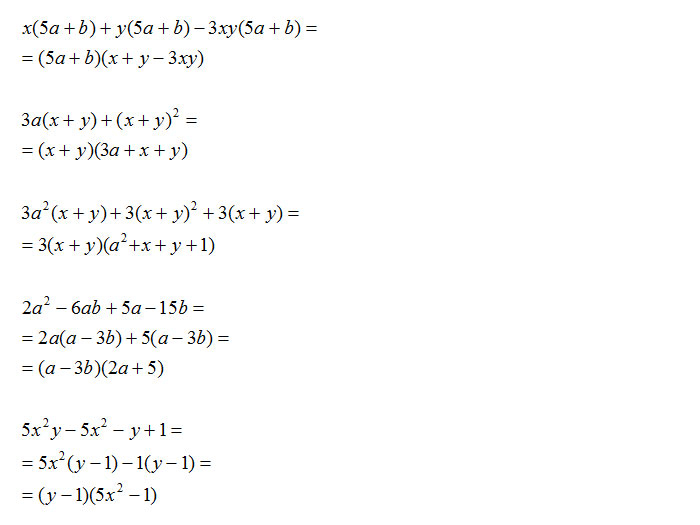
Come puoi vedere dagli esercizi svolti non è necessario che sia un unico monomio l’elemento comune, ma può essere anche una parentesi intera. Nel caso in cui devi svolgere esercizi con il raccoglimento con le frazioni ricordati di seguire semplicemente la regola: MCD e poi divisione di polinomi ed eviti di sbagliare.
Come ultima cosa di questa lezione vi lasciamo con degli esercizi con soluzioni sul raccoglimento a fattor comune. In caso di problemi il nostro staff resta a vostra disposizioni per chiarimenti o lezioni individuali: contattaci!
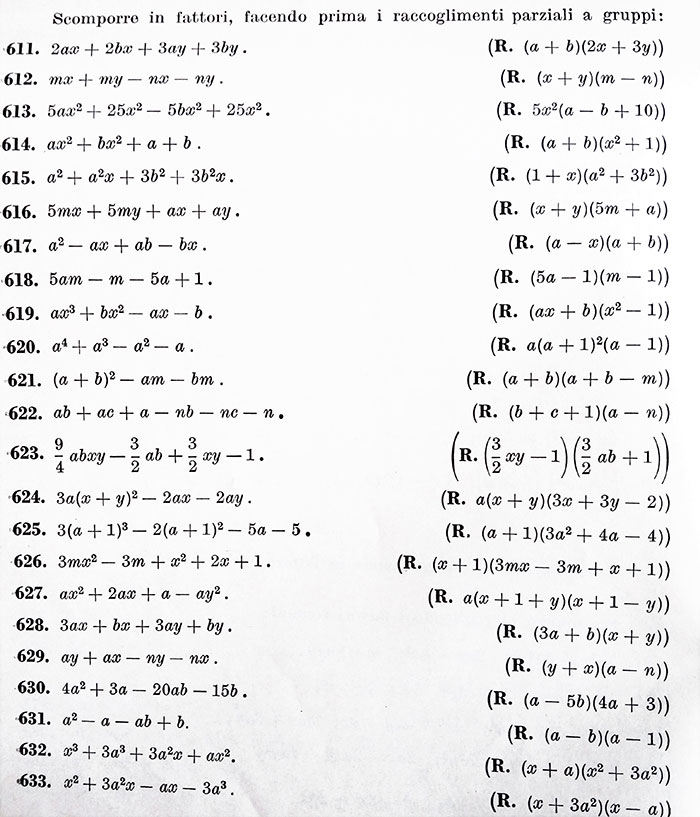
Grazie siete veramente umani e comprensivi. Date delle spiegazioni veramente esaurienti. Senza di voi siamo persi.
CONTINUATE COSì VE NE SAREMO VERAMENTE GRATI A VITA. Stella sCOPACASA
È molto difficile trovare dei buoni esercizi di algebra su cui far pratica, ma qui ne trovo sempre di adatti e utili. Grazie mille e fighting!