Logaritmo naturale – proprietà, esercizi e regole da conoscere riassunte in una facile mini-guida

Il logaritmo naturale è un logaritmo che ha alla base il numero di Nepero e. In matematica si esprime con il simbolo ln. In questa lezione vedremo tutto ciò che riguarda il logaritmo naturale, dal grafico alle sue proprietà. Iniziamo subito con la definizione matematica.

Nella lezione sulla definizione di logaritmo, abbiamo detto che un logaritmo si esprime nella forma:

log_ab = c

Nel logaritmo naturale si sottintende la base e si esprime tutto nella forma:

lnb = c

Proprietà del logaritmo naturale

In questo capitolo vedremo riassunte in breve quali sono le proprietà dei logaritmi naturali. Ti potrai subito accorgere che non c’è alcuna differenza con i logaritmi con base generica. Per approfondire l’argomento, ti consigliamo di leggere il nostro articolo sulle proprietà dei logaritmi. Troverai le varie regole spiegate passo passo con tanti esempi pratici.

lna+lnb=ln(a·b)

lna-lnb=ln(a:b)

lna^b=b·lna

Approfondimento: come si fa la somma di logaritmi

Logaritmo naturale di e

Che cosa succede quando si ha di fronte lne? Nella lezione sulle regole base dei logaritmi abbiamo già parlato del fatto che quando base e argomento hanno lo stesso valore, il risultato del logaritmo è pari a 1. Quindi quando ci troviamo di fronte al logaritmo naturale di e la situazione non cambia, il risultato è sempre 1. Per cui possiamo scrivere:

lne=1

Logaritmo naturale di 0

Abbiamo dedicato un intera lezione al logaritmo di zero. Abbiamo dato due diverse motivazioni che ci portano a dire che il risultato di questa operazione matematica è impossibile. Quando la base è il numero di Nepero, la situazione non cambia. Per cui possiamo scrivere che:

ln0=IMPOSSIBILE

Logaritmo naturale di 1

Una caratteristica comune di tutti i logaritmo è quella di assumere valore 0 quando l’argomento è 1. Questa proprietà vale per i logaritmi naturali, per quelli con base maggiore di 1 e con quelli con base compresa tra 0 e 1. Giustificheremo questa affermazione andando ad analizzare il grafico del logaritmo naturale. Intanto possiamo già scrivere che:

ln1=0

Logaritmo naturale di infinito

Abbiamo dedicato una lezione proprio per capire quanto fa il logaritmo di infinito. Avevamo detto che il risultato è proprio infinito: col segno più se la base è maggiore di 1, col segno meno se la base è compresa tra 0 e 1. Poiché il numero di Nepero è un numero maggiore dell’unità, allora possiamo dire che:

ln∞=+∞

Grafico logaritmo naturale

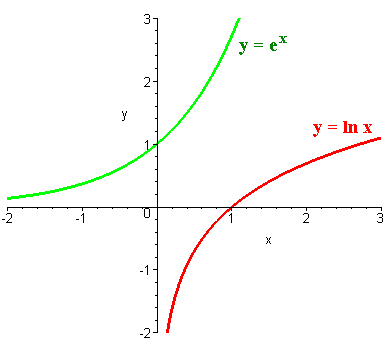
Grafico del logaritmo naturale e dell’esponenziale naturale

Come puoi vedere dal grafico, la curva rossa che rappresenta il logaritmo naturale, ha un andamento che ricorda in tutto e per tutto quello dei logaritmi con base maggiore di 1. Per completezza sul grafico ti abbiamo riportato anche l’andamento in verde dell’esponenziale naturale.

Puoi vedere che le curve sono perfettamente simmetriche. Questo perché il logaritmo naturale è la funzione inversa dell’esponenziale naturale. Matematicamente questo si esprime come:

y=f(x)=lnx → y^-1=f^-1(x)=e^x

Esercizi svolti

Esempio 1)

ln(x-1)=3

Attenzione perché in questo esercizio c’è anche la x. Quindi non è un semplice logaritmo naturale, ma un’equazione logaritmica. Per risolverla bisogna rendere tutto in forma esponenziale a base e.

e^ln(x-1)=e³

x-1=e³

x=e³+1

Esempio 2)

ln(lne)

In questo esercizio dobbiamo risolvere il logaritmo naturale del logaritmo naturale. Non facciamoci prendere dal panico guardandoci intorno chiedendoci come si fa. E’ molto semplice:

= ln(1) = → il logaritmo naturale di e abbiamo detto essere pari a 1

= 0 → il logaritmo naturale di 1 abbiamo detto essere pari a 0