Partendo dalla definizione di mcm, Impareremo come si calcola il minimo comune multiplo. troverai in questa lezione degli esercizi svolti e tanti suggerimenti per eliminare definitivamente ogni dubbio.
Gli argomenti della lezione
- Introduzione: le difficoltà degli studenti
- Definizione di minimo comune multiplo
- Come calcolare minimo comune multiplo
- A che serve e perché è così importante
- Esempio 1
- Esempio 2
- Esempio 3
- Motodi veloci di calcolo e consigli
- Esercizi da risolvere
Introduzione
Nelle varie espressioni algebriche che hai risolto fino a questo momento abbiamo provato a risolvere operazioni con le frazioni, dando per scontato che sapessi come si calcola il minimo comune multiplo, un concetto che si impara in realtà già in aritmetica.
Molto spesso in realtà i nostri studenti, soprattutto nei compiti in classe mostrano paura e molte difficoltà su questo argomento perché non hanno ben chiaro come si calcola il minimo comune multiplo, per cui in questa lezione daremo una precisa definizione, svolgeremo assieme degli esercizi così da non avere più problemi neanche quando in futuro applicheremo l’argomento alle equazioni e disequazioni.
Minimo Comune Multiplo definizione
Il minimo comune multiplo (si scrive anche mcm) è il più piccolo numero che sia divisibile per tutti i numeri dati.
Che significa? Se io ho tre numeri, il mcm è, tra i tanti possibili divisori, il più piccolo.
Immagino che la definizione di mcm da sola non sia riuscita a farti comprendere molto sull’argomento. E’ normale, non preoccuparti. Continua a leggere e vedrai che ti sarà tutto più chiaro.
Come si calcola il minimo comune multiplo
Per calcolare il mcm si prendono i fattori comuni e non comuni, presi una sola volta con il massimo esponente.
Con questa definizione sul calcolo mcm in matematica, che siamo sicuri imparerai col tempo a memoria, si fa però una premessa. Cioè che tu abbia già studiato e sappia fare la scomposizione in numeri primi.
Tornando alla nostra domanda principale, cioè come si fa il minimo comune multiplo, il modo migliore per comprendere l’enunciato è con degli esempi pratici. Proviamo ad esempio a calcolare il minimo comune multiplo tra 20 15 30.
Si inizia con la scomposizione in numeri primi dei tre dati da traccia. Per cui si ottiene:
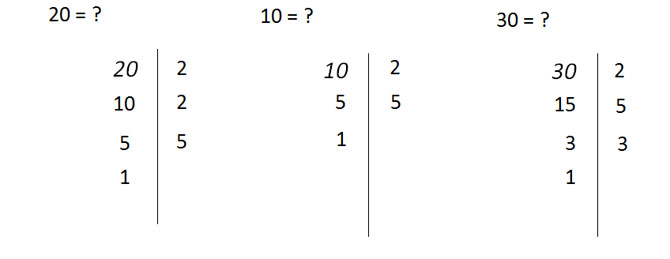
Come si calcola il minimo comune multiplo?
A questo punto riepilogando ottenuti scomponendo i numeri in fattori primi, usando le potenze posso scrivere:
20=22x5
15=5×3
30=2x5x3
Completata la scomposizione in numeri primi, guardo ora solo i termini a destra dell’uguale, cioè i fattori – ti ricordiamo che si chiamano così “i numeri che sono moltiplicati tra loro”.
Il trucco che ci suggeriamo di darvi è di cerchiare sul foglio su cui vi esercitate i termini che contribuiscono al calcolo del mcm. Esattattamente come vedi nella prossima immagine.
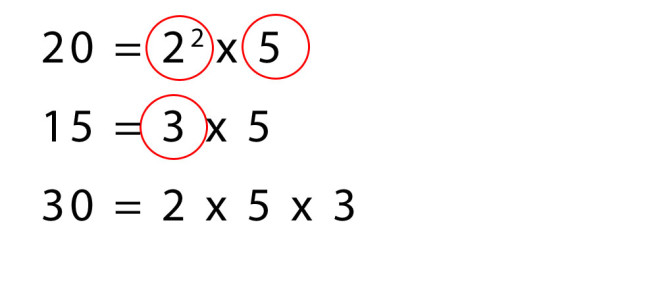
Attenzione ai termini evidenziati!
Quali termini abbiamo cerchiato in rosso? Le regole sono semplici:
- ogni fattore va cerchiato una sola volta, ecco perché il 5 e il 3 compaiono solo una volta con il cerchietto.
- tra due fattori uguali si sceglie quello con il grado massimo – quindi tra 2 al quadrato e 2, si sceglie quello con la potenza più alta.
Se ti stai chiedendo, in tutto ciò, come si calcola il minimo comune multiplo, sappi che hai praticamente fino. Ti basta semplicemente moltiplicare i fattori che hai evidenziato e calcolare il risultato finale:
mcm=22 x 5 x 3=60
L’esercizio è così concluso. Tornando un attimo alla definizione di mcm, abbiamo detto che questo è che il più piccolo numero divisibile tra i tre assegnati. Immaginiamo infatti di voler trovare un numero che sia divisibile per 20, 15 e 30. Aiutandoci con una calcolatrice scopriamo che tra questi numeri il primo è 60 – visto che 60 possiamo dividerlo sia per 20, sia per 15 sia per 30 – poi abbiamo 120, 180, eccetera. Il più piccolo di questi è certamente 60, da cui la definizione di mcm.
A che serve il minimo comune multiplo?
La domanda è certamente legittima, ma se hai già avuto modo di affrontare un esercizio con le frazioni, avrai certamente notato che il mcm è fondamentale per calcolare la sottrazione e la somma di frazioni. Ci servirà inoltre, più avanti, quando dovremo risolvere le equazioni fratte e le disequazioni fratte, per cui è importante che tu abbia capito bene l’argomento. Proprio per questa ragione, ti presentiamo ora altri esempi che possiamo risolvere assieme. Prendi carta e penna e seguici nei calcoli.
Minimo comune multiplo esercizi
Di seguito troviamo alcuni esempi per mettere in pratica la teoria vista fino a questo momento. Puoi trovare una raccolta di esercizi risolti a questo link: mcm e mcd esercizi e problemi svolti
Esempio 1
Calcolare il minimo comune multiplo dei numeri 270, 144 e 224.
Iniziamo come sempre a scomporre in fattori primi i numeri datici dalla traccia:
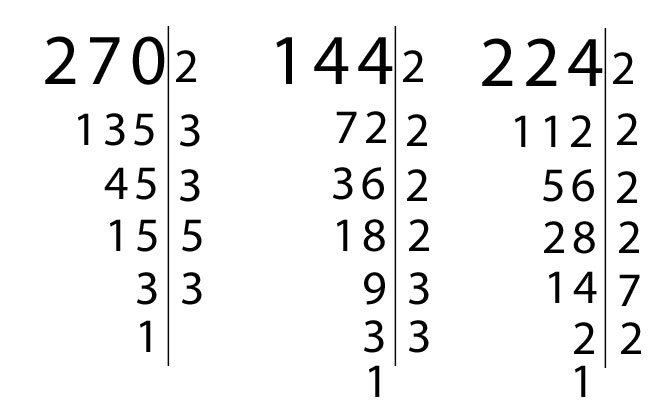
A questo punto mi scrivo in maniera più compatta i risultati ottenuti con la scomposizioni in numeri primi:
270=2 x 32 x 5
144=24 x 32
224=25 x 7
Prova cerchiare tu questa volta i fattori presi una sola volta con il massimo esponente. Dovrai così cerchiare 2 elevato a 5, 3 elevato a 2, infine 5 e 7 che compaiono senza potenze. Puoi così scrivere, per il calcolo del mcm, che:
mcm=25 x 33 x 5 x 7 = 30240
Per fare la verifica del minimo comune multiplo, basta che dividi il risultato finale, in questo caso 30.240, per i tre numeri dati dalla traccia. Se le tre divisioni escono tutte senza la virgola, allora il risultato è corretto.
Esempio 2
Quello che vi proponiamo di risolvere assieme, ora, è un esercizio con semplici operazioni con i numeri relativi fratti, così che sia chiaro a che serve il minimo comune multiplo, almeno in questa prima parte del programma:
+3/12 – 4/15 + 1=
Iniziamo calcolando il minimo comune multiplo tra i tre denominatori. NOTA BENE: se uno degli addendi non ha la frazione, è sottinteso che il denominatore sia 1.
+3/12 – 4/15 + 1/1=
Scompongono 12, 15 in numeri primi. 1 posso anche ignorarlo…
12=22 x 3
15=5 x 3
mcm=5 x 3 x 22 = 60
A questo punto risolvo la frazione inserendo un solo denominatore comune, il minimo comune multiplo appena calcolato, così da poter scrivere:
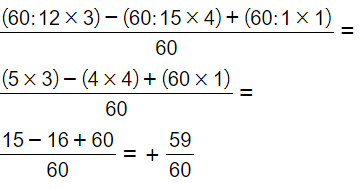
In questo esercizio in realtà la seconda frazione, cioè 3/12, poteva essere semplificata: dato che 12:3=4, avrei più comodamente scrivere al posto di 3/12, la frazione 1/4. Il risultato sarebbe stato comunque lo stesso, ma avrei ridotto i calcoli. Attenzione: prova sempre a semplificare le frazioni! Ti semplificherà la vita…
Esempio 3
Un esercizio conclusivo più semplice: calcolare il minimo comune multiplo tra 50 e 150.
Questa volta lasciamo a voi la scomposizione in fattori primi con lo schema verticale, sarà un buon allenamento. Noi vi indichiamo direttamente i risultati del calcolo:
50 = 2 x 52
150 = 2 x 52 x 3
Cerchia i termini utili per il calcolo del mcm così come abbiamo fatto negli esercizi precedenti e potrai così trovare:
mcm= 2 x 52 x 3
E’ vero che questo esercizio era più semplice, ma non era possibile risolverlo in maniera più rapida e diretta?
Calcolare il minimo comune multiplo in maniera diretta
Ecco un semplice trucco da ricordare per calcolare il minimo comune multipolo: verifica sempre che i numeri di cui vuoi calcolare il mcm siano tra loro divisibili. Il più piccolo dei due puoi anche ignorarlo!
Nel nostro esempio infatti avevamo 50 e 150. Ma 150:50=3. Questo significa che i due numeri sono tra loro divisibili. Possiamo così ignorare 50, per il calcolo del mcm. Ci resta solo 150. Il minimo comune multiplo è quindi 150.
E se avessimo avuto più numeri? Ad esempio 50, 70, 150? Nessun problema. Poiché 150 è divisibile per 50, quest’ultimo possiamo ignorarlo. Ma dato che 150 e 70 non sono tra loro divisibili allora il calcolo diretto si ferma. Dovremo ora solo calcolare il mcm tra 150 e 70 nella maniera vista sopra. Ad ogni modo, con questo semplice trucco, abbiamo ridotto notevolmente i calcoli da eseguire.
Esercizi sul mcm da risolvere

Risolti questi esercizi, non dovremmo più avere problemi con le frazioni. Puoi a questo punto passare ad esercizi più complessi come le espressioni algebriche.
Come sempre per dubbi o per chiarimenti, restiamo a tua completa disposizione. Contattaci!
Grazie questo sito e grandioso piu dei altri prima non sapevo come si faceva ma con questo sito o capito tutto e per questo do 5✨ stelle
Sono d’accordo con te!
Anch’io non capivo e la prima volta mi sembravano numeri scelti a caso che poi vengono moltiplicati.
Ciao riesci a fare le espressioni
Ciao Gioia,
trovi le espressioni a questo link: ESPRESSIONI ALGEBRICHE
Grazie Angela,
siamo contenti che il nostro lavoro sia di tuo gradimento. Continua a seguirci allora e a studiare la matematica con noi! 😉
Ottima risorsa, a quando la pagina sul Massimo Comune Divisore? 😀
Grazie Stefano, il vostro apprezzamento è fondamentale per noi. Volevi il mcd? Eccolo qui, proprio su richiesta –> Come calcolare il massimo comune divisore
Grazie mille!