Nel paragrafo dedicato alle proprietà dei logaritmi abbiamo già parlato di come se eseguano le operazioni matematiche fondamentali tra logaritmi. In questa lezione faremo un approfondimento che riguarda la somma di logaritmi. Iniziamo facendo una rapido riassunto di quanto ci siamo già detti.
Somma di logaritmi
Come si fa l’addizione tra logaritmi? Per rispondere a questa domanda basta seguire la formula:
![]()
REGOLA: La somma di logaritmi è un logaritmo che ha per base la stessa base e per argomento il prodotto degli esponenti.
In parole povere assicurati che i logaritmi da sommare abbiano la stessa base così che puoi riscrivere il logaritmo mantenendo la base e semplicemente moltiplicando gli argomenti. Per esempio:
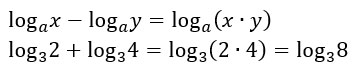
ATTENZIONE: non confondere la somma di logaritmi, con il logaritmo di una somma! Quest’ultimo caso – ad esempio log(x+y) non può essere risolto.
Somma di logaritmi con base diversa
Fin ora niente di complicato. Cosa succede se invece devo fare l’addizione di logaritmi che hanno base differente? In quel caso è necessario modificare una delle due basi, così da riportarci nella situazione precedente. Per far ciò ti consigliamo di segnarti la formula per il cambiamento delle basi dei logaritmi.
E’ indifferente quale dei due logaritmi viene cambiato di base, la cosa importante è che la somma di logaritmi avvenga sempre con la stessa base.
Esempio 1.
Un caso che spesso ci viene chiesto: come si fa quando ho la somma di logaritmi con lo stesso argomento? Se hanno la stessa base si risolve in pochi semplici passaggi. Vediamo subito praticamente come calcolare l’addizione:
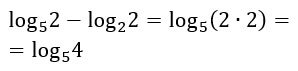
L’esercizio si conclude qui perché non sono possibili altre semplificazioni.
Esempio 2.
Vediamo come si fa la somma di logaritmi con base diversa, applicando le formule studiate fino ad ora.
![]()
Trasformiamo il logaritmo in base 5 in logaritmo in base 3.
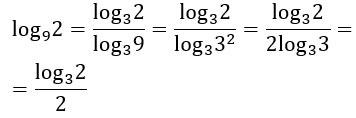
Nell’ultimo passaggio hai capito perché abbiamo eliminato il termine log33? Perché quando base e argomento sono uguali, il logaritmo fa 1. E 2×1 fa 2. Quindi a denominatore resta solo 2. A questo punto la mia somma di logaritmi diventa:
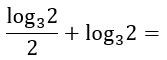
Ma questa non è più una normale addizione, visto che c’è una frazione. Per questa ragione è necessario fare un banale minimo comune multiplo (mcm=2) per ottenere
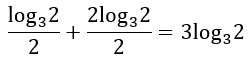
Esempio 3.
Un nostro studente ci ha chiesto, durante una lezione, come si risolve la somma di logaritmi con la x prima di uno dei due addendi. Vediamo il caso più nel dettaglio.
![]()
Sicuramente non possiamo immediatamente risolvere il logaritmo come se fosse una semplice somma numerica, perché è coinvolta anche la x. Quindi non è più un’espressione ma un’equazione, a cui in questo caso manca il secondo membro. Tuttavia in questo caso si possono sfruttare le regole sui logaritmi per fare qualche semplificazione.
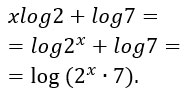
Negli ultimi due passaggi è stata semplicemente applicata la formula per la somma di logaritmi.
Più di questo, però, in questo esercizio non possiamo fare perché come detto non si tratta più di un’espressione, ma di un’equazione logaritmica in cui manca il secondo membro, per cui dobbiamo fermarci qui.
Considerazioni conclusive
Le somme di logaritmi sono estremamente facili da risolvere. Si tratta di una piccola moltiplicazione tra gli argomenti degli addendi da sommare. Tuttavia la cosa che fa cadere spesso in errore gli studenti durante i compiti e verifiche è la contestualizzazione della regola assieme alle altre.
Cosa significa? Che non basta saper applicare la somma di logaritmi, ma è importante conoscere e saper applicare anche tutte le altre regole che riguardano i logaritmi, specialmente quella sulla potenza, utilizzata molto spesso per eliminare i coefficienti numerici.
Forse potrebbe interessarti anche: differenza di logaritmi – formula ed esercizi svolti