La più classica delle domande che si pone ogni studente quando si trova ad affrontare i logaritmi è: che cos’è il Numero di Nepero? Generalmente il professore di matematica dà sempre la stessa risposta: è una costante, non preoccupatevi di lui perché non vi da fastidio nei calcoli. Allora lo studente replica: “Si ma quanto vale il numero di Nepero?” In questa lezione faremo un po’ di chiarezza, cercando di darti una spiegazione ed una definizione che sia facile e che allo stesso tempo risolva ogni tuo dubbio.
Che cos’è il numero di Nepero?
Il numero di Nepero è una costante matematica indicata generalmente con la lettera e. Viene anche chiamata numero di Eulero ed è numero irrazionale trascende, cioè non si può esprimere con una frazione né come un numero con la virgola periodico. Questa caratteristica lo rende molto simile al PI GRECO.
Quanto vale il Numero di Nepero allora? E’ un numero positivo e vale 2,718, approssimando per eccesso a tre cifre decimali. In realtà ti accorgerai, risolvendo i vari esercizi sui logaritmi e sugli esponenziali che non è importante conoscere il valore del numero di Nepero.
Definizione e dimostrazione
Per comprendere la definizione del numero di Nepero sono necessarie conoscenze avanzate della matematica, che vanno dai limiti alle equazioni differenziali. Mentre i primi si studiano, generalmente, nel programma di analisi, cioè al 5 anno del liceo, le equazioni differenziali si studiano solo all’università di fisica, matematica ed ingegneria. Noi ti riportiamo comunque, per curiosità la definizione più usata dagli studenti.
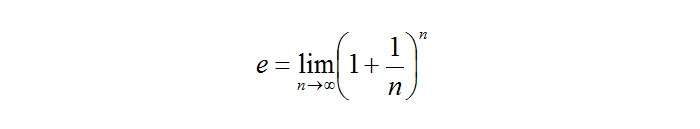
La formula che hai appena visto non è altro che il limite notevole del Numero di Nepero. Chi ha studiato il programma di analisi sa benissimo quanto i limiti notevoli siano importanti nello studio di funzione. Questa espressione venne usata per la prima volta da Bernulli, matematico del XVIII secolo. Se proviamo a sostituire dei valori al posto della n, vediamo quali sono i risultati.
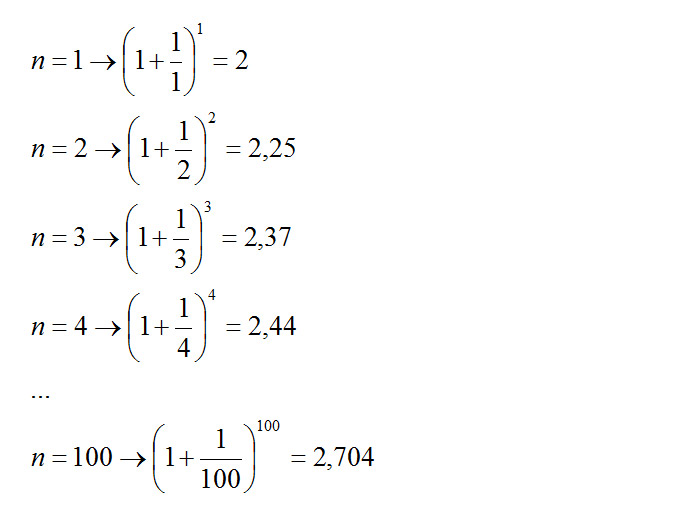
Quello che si nota è che più aumenta n, più il risultato finale si avvicina al reale valore del numero di Nepero, che viene quindi raggiunto solo quando n tende ad infinito.
La storia del numero di Nepero
Quello di cui stiamo parlando oggi è un numero molto importante, quanto il PI GRECO, ma fuori dall’ambiente matematico sono in pochi a comprenderne il valore. L’uso del Numero di Nepero è fondamentale nelle operazioni di matematica finanziaria. Su un’antica tavoletta babilonese ( siamo nel 1.700 a.C.) uno studioso si chiedeva quanto tempo tesse volerci ad una somma economica per raddoppiare se ogni anno aumentava del 20%. Per risolvere questo semplice esercizio i babilonesi avrebbero dovuto usare le equazioni esponenziali, che ancora non conoscevano.
Il numero e nasce molto probabilmente nel XVII-XVIII secolo, un’epoca in cui si stavano per avviare le grandi rivoluzioni industriali e c’era un grande interesse per il capitale e sui possibili guadagni. Il primo ad avvicinarsi molto al valore di questa costante matematica fu Bernulli che calcolò una cifra compresa tra 2 e 3. Prima di lui altri avevano provato, come John Napier (in italiano Giovanni Nepero) a cercare un nuovo valore da assegnare alle basi dei logaritmi. Solo dopo la sua morte uscì un lavoro in cui la costante matematica venne chiamata con il nome che noi tutti oggi conosciamo.
Le applicazioni del numero di Nepero
Una volta capito che cos’è, cerchiamo ora di capire a cosa serve il numero di Nepero. Oltre ai calcoli possibili nella matematica finanziaria con gli interessi composti e le capitalizzazioni, le possibili applicazioni della costante di Nepero sono moltissime: dal calcolo delle probabilità allo studio di funzioni, dalla formula di Eulero usata per i numeri immaginari alla più semplice risoluzione delle equazioni logaritmiche.
Ritengo che la storia del numero e sia piacevole ed interessante, ma ancora non è chiaro perché oltre la base 10 dei logaritmi di Briggs o decimali o volgari, (e anche base 2 , 3 ,5 ecc. ) si usano logaritmi in base e neperiano. Si capiscono le difficoltà di calcolo. Una cosa è trovare l’esponente da dare a 10 per trovare 100 (ad esempio 2: infatti log di 100 in base 10 è 2; e una cosa è trovare l’esponente da dare a e per ottenere 100 (che approssimato alla nona cifra decimale vale 4,605170186). Dunque perché questo numero trascendente, illimitato, non periodico, che non si classifica come irrazionale come quello derivante ad esempio dalla radice quadrata di 2, che vale approssimato alla nona cifra decimale 1,414213562.
Sarei contento di una spiegazione valida. Altro discorso riguarda pi greco. Esso è la metà del rapporto incommensurabile tra lunghezza della circonferenza e il raggio. Lunghezza di C= 2 x pi greco x raggio. Esso si ricava facendo tendere al minimo l’angolo compreso tra due raggi, in modo da ottenere quanto più è possibile un triangolo rettangolo e confondere la corda con l’arco di circoferenza interessato. Il prodotto di 180 o 360 o 720 per il seno dell’angolo considerato mi dà via via un’approssimazione sempre più spinta del valore di pi greco. Di solito posto dai ragazzi uguale a 3,14. Aspetto vostre notizie.
Credo che una possibile spiegazione si trovi nel fatto che la funzione esponenziale in base e sia autofunzione dell’operazione di derivazione. Quindi è semplicemente quel numero che semplifica enormemente il calcolo differenziale e tutte le teorie costruite su di esso.
consentitemi di suggerire/ipotizzare che è anche il Numero che la Natura ha riservato agli umanI per venire al mondo dal momento della fecondazione .Come si sarebbe espressa la Natura?
Consideriamo il valore medio del periodo di 9 mesi e di 7 mesi la finestra temporale per uscire, senza l’intervento della tecnica , dal grembo della donna. Consideriamo i giorni che nel caso di 9 mesi è di 6480 ore mentre nel caso di di 8 mesi è di 5760 ore e nel caso di 7 mesi(limite inferiore) 5040 ore .
Noteremo che per i 7 mesi si ha : e= (1+5040/5040)^5040)= 2,718,012..
8 mesi >>>. e=( 1+5760/5760)^5760)= 2,718,045..
9 mesi>>>>. e=( 1+6480/6480)^6480)=. 2,718,072..
Faccio notare che nel casi dei parti di 6 mesi deve intervenire la tecnica con i suoi mezzi per far nascere la creatura che la Natiura considera immatura; infatti nella formula che riguarda i nati di sei mesi non si raggiunge il limite 2,718 ma è inferiore e pari a ;e= (1+4320/4320)^4320=2,717 967..
li, (1 -2-22)
Esempio che ricorda il dito, osservato dallo sciocco, del saggio che indica la luna.
quando n supera 3000, il valore della funzione ha le prime 3 cifre decimali uguali a quelle del numero di Nepero. La Natura non ha riservato nessun numero agli umani per venire al mondo.
L’osservazione sul numero di ore in 6 mesi di gestazione, 4320, considerati innaturali e bisognosi dell’intervento della tecnica è ridicola: se si considerano i mesi, la tecnica dovrebbe intervenire sempre (n=9 valore funzione 2.581……, mentre se si considerano i minuti primi, la nascita sarebbe da considerare naturale anche dopo un mese (30 giorni*24 ore*60 minuti= 43.200 minuti – valore funzione 2.718….)