L’arcoseno di x non è altro che la funzione inversa del seno applicata alla variabile x. E’ in genere un argomento che gli studenti considerano difficile, per cui ci soffermeremo cercando di rendere la spiegazione semplice e alla portata di tutti.
Per capire quali sono le proprietà dell’arcoseno e vederne il grafico, è necessario che alcuni concetti siano noti. Ovviamente bisogna conoscere la funzione seno, altrimenti non possiamo studiarne l’inversa, e sarebbe opportuno conoscere il concetto di funzione biunivoca.
In linguaggio matematico la funzione arcoseno si indica con i simboli arcsin(x) oppure arcsen(x), a seconda del testo e della notazione utilizzata. Entrambi sono tuttavia parimenti validi.
La funzione y = arcsin x
Dominio e codominio – la premessa
Prima di vedere operativamente che cos’è l’arcoseno di x, è importante fare una premessa. La funzione y=sen(x) non è biunivoca perché un valore di y appartenente al codominio [-1;+1] è immagine di infiniti valori di x, ossia ci sono infiniti archi sulla circonferenza goniometrica che hanno lo stesso seno.
Poiché la funzione non è biunivoca, allora non è invertibile. Quini in linea teorica non si potrebbe neanche parlare di arcoseno. Tuttavia, se effettuiamo una restrizione della funzione y=senx, ossia consideriamo il sottoinsieme I={-π/2;+π/2} del suo insieme di definizione R e la sua immagine f(I)=[-1;+1], la funzione f risulta biiettiva tra gli insiemi I e f(I) e quindi relativamente a tali insiemi esiste la funzione inversa f-1.
Approfondimenti: quando una funzione è invertibile?
Che cos’è l’arcoseno
A questo punto siamo pronti per dare una spiegazione sull’arcoseno: è la funzione inversa del seno e si indica con:
x= f-1(y)=arcsin y
da cui, scambiando le variabili, si ha:
y= f-1(x)=arcsin x
Dominio arcoseno (e codominio)
Questa funzione inversa del seno ha il dominio D l’insieme che abbiamo precedentemente indicato con f(I). Per cui il dominio D=[-1;+1]. Il codominio invece è quello che precedentemente abbiamo indicato con I={-π/2;+π/2}.
Grafico arcoseno
Per disegnare il grafico dell’arcoseno è bene aver presente com’è fatta la sinusoide.
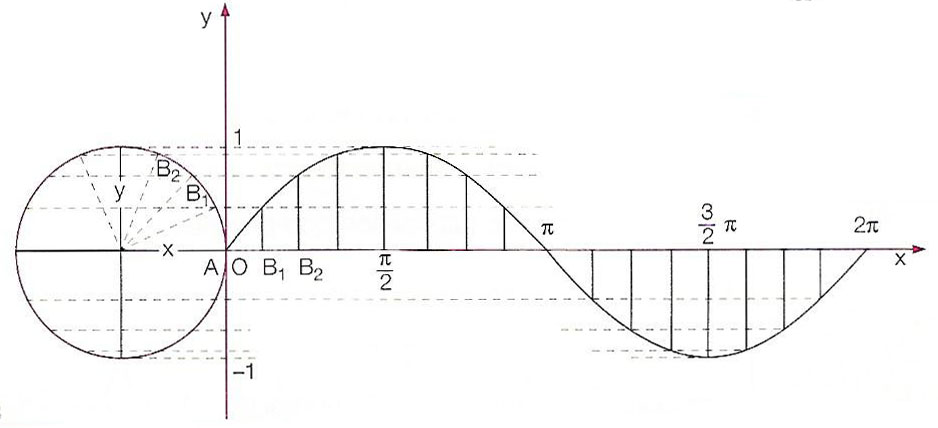
Sinusoide – il grafico del seno
Arcoseno grafico: per disegnarlo dobbiamo il simmetrico della funzione f di partenza (in questo caso il seno) rispetto alla bisettrice del primo e terzo quadrante. Per aiutarti a comprendere come si costruisce grafico arcsin x, ecco i vari passaggi.
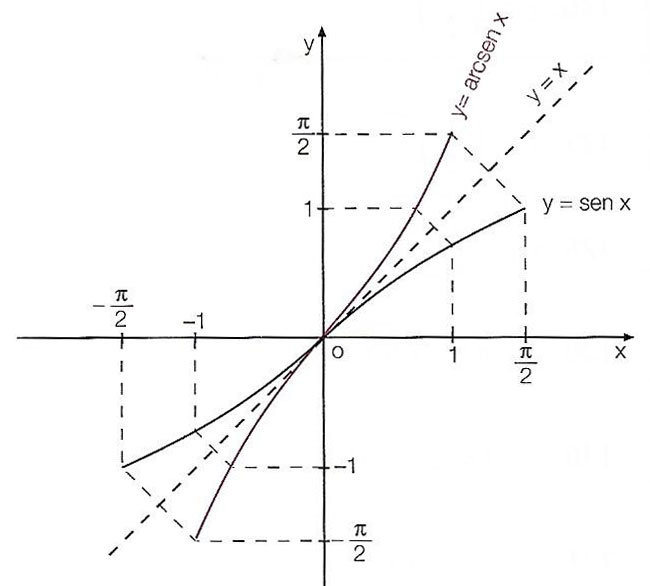
Nell’immagine sopra ti abbiamo mostrato come costruire iniziare a costruire il grafico dell’arcoseno. Proseguendo con il disegno si ottiene quindi il grafico completo.
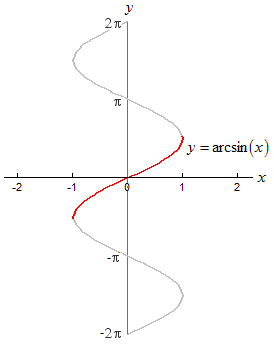
Del grafico dell’arcoseno si considera solo la zona rossa
Come calcolare arcsin x – esempio pratico
Per il calcolo dell’arcoseno puoi ricorrere alla calcolatrice, ma è difficile che questa ti restituisca un valore accettabile visto che generalmente lo ha già moltiplicato per pigreco.
Approfondimenti: come calcolare l’arcoseno con la calcolatrice
Molto meglio ragionare come segue:
- per trovare l’arcsen x devo chiedermi qual è l’angolo il cui seno è proprio pari a x.
Facciamo un esempio e proviamo a calcolare arcsen x, con x=1/2.
arcsen(1/2) → dobbiamo trovare l’angolo il cui seno vale √3/2. Sappiamo che il seno di 60 vale proprio √3/2, così come anche sen120°. Tuttavia abbiamo premesso Questo vuol dire che:
arcsen(1/2)=60° e 120° → Tuttavia ricordi cosa abbiamo detto? Che il codominio (cioè l’intervallo sull’asse delle y in cui la funzione è definita) varia tra -π/2 e +π/2. Quindi 120° (2/3 π) non va incluso nei risultati perché maggiore di π/2. Il risultato è quindi:
arcsen (1/2)=60°
e, volendo esprimere l’angolo in radianti, possiamo scrivere che:
arcsin (1/2) = π/3
Proprietà dell’arcoseno
Avendo visto subito quali sono dominio e codominio, possiamo fare un’osservazione piuttosto semplice: l’arcoseno si ripete così come faceva il seno, ma questa volta in senso verticale. Per questa ragione non si può dire che l’arcoseno sia una funzione periodica.
Ricordi che cos’è una funzione matematica? E’ una relazione che associa ad un elemento della x, uno ed un solo elemento della y. Se provi a guardare l’ultimo grafico dell’arcoseno, noti che quando ad esempio x=1, ci sono vari valori della y. Per questa ragione il grafico non rappresenta una funzione ed è per quella stessa ragione che è stata necessaria la premessa con dominio e codominio.
Simmetrie
Si nota una simmetria della funzione rispetto all’origine degli assi, per cui possiamo dire che l’arcoseno è dispari. Matematicamente ciò si esprime attraverso la relazione:
f(x)=-f(-x)
Intersezioni con gli assi
Dal grafico dell’arcoseno puoi immediatamente capire come ci sia una sola intersezione con l’asse delle ascisse nel punto di coordinate cartesiane 0(0;0), cioè nell’origine. Tenendo conto che la y può essere solo compresa tra -π/2 e +π/2, allora appare evidente che non ci sono altre intersezioni da prendere in considerazione.
L’arcoseno è una funzione crescente?
Se consideriamo l’intervallo indicato della y (e quindi solo la parte rossa del grafico in figura), allora la funzione arcoseno è monotona strettamente crescente su tutto il suo dominio. Questo vuol dire che da quando parte da x=-1 a x=+1 la funzione cresce sempre e nessuna y è mai uguale alle precedenti.
Alcuni esercizi svolti
- arcsin [sin (x)] = x
Si tratta di un’espressione breve che è bene ricordare. Applicare la funzione inversa alla funzione stessa, mi dà come risultato l’argomento. Quindi in termini matematici f-1[f(x)]=x, per cui l’arcoseno del seno è proprio pari alla x.
- sin [arcsin x] = x
Si tratta del caso perfettamente analogo al precedente. C’è una rapida successione della funzione e della sua inversa, per cui il risultato è pari proprio all’argomento, cioè alla x.
- Provare a disegnare il grafico y=arcsin(-x)
L’esercizio si risolve facilmente andando a ribaltare intorno all’asse y il grafico dell’arcoseno che abbiamo visto prima. Il risultato sarà quindi:
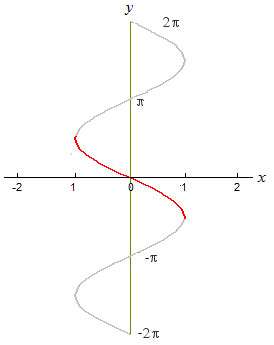
grafico arcsin -x
Per esserne convinti, proviamo ad assegnare 3 valori alla x (-π/2 ; 0 ; +π/2) e prova a calcolare l’arcoseno. Vedrai che otterrai i valori che sono presenti sul grafico.
Conclusioni
Come puoi vedere la spiegazione dell’arcoseno non è molto complessa, ma ci sono alcune cose che vanno ricordate, come la restrizione del codominio tra -π/2 e +π/2. Purtroppo per calcolare arcsin x la calcolatrice non sempre ci è d’aiuto, ma con la tecnica che abbiamo visto, si può eseguire il calcolo dell’arcoseno a mente (se si tratta ovviamente di valori di seno e coseno di angoli noti).
Per ulteriori chiarimenti o dubbi, lascia pure un commento alla lezione. Il nostro staff sarà felice di risponderti.