Come si calcola il seno di 60 gradi? Sulla calcolatrice mi da come risultato 0,5, ma non capisco come poter ottenere questo stesso risultato a mente senza impararlo a memoria. E’ possibile inoltre avere una dimostrazione? Grazie – Stefania.
Ringraziamo Stefania per averci scritto via mail manifestandoci i suoi dubbi e i suoi problemi su questa prima parte del programma di trigonometria. Imparare a memoria il valore di seno e coseno di angoli noti è infatti è una delle difficoltà maggiori degli studenti. Sono pochi quelli infatti che riescono a memorizzare subito il valore del seno di 60 gradi o il seno di 45° senza ricorrere a tabelle o prontuari.
In questa lezione vedremo nel dettaglio come si ricava il seno di 60°. Innanzitutto, come ci ha scritto Stefania, si tratta di un calcolo che si può fare anche con la calcolatrice anche se bisogna saper interpretare il risultato. Troverai in tutte le tabelle con i valori di seno e coseno scritto che:
Il seno di 60° è infatti uguale a radice quadrata di tre fratto due (radical tre mezzi) che la calcolatrice ti indicherà come 0,866. Molto spesso ti capiterà di trovare la misura dell’angolo in radianti, per cui possiamo anche scrivere che:
senπ/3=(rad3)/2
Se non ricordi come si passa da 60° a π/3, dai un’occhiata alla nostra lezione sulla conversione gradi radianti. A questo punto o ricordi il valore a memoria, ma è duro riuscire a farlo con tutti gli angoli, oppure leggi come si ricava in maniera semplice.
Seno 60 gradi – come si ricava?
Iniziamo disegnando la circonferenza goniometrica, quindi che ha centro nell’origine e raggio unitario. Su questa andiamo a disegnare l’angolo di 60° partendo dall’asse delle x e con una rotazione in senso antiorario.
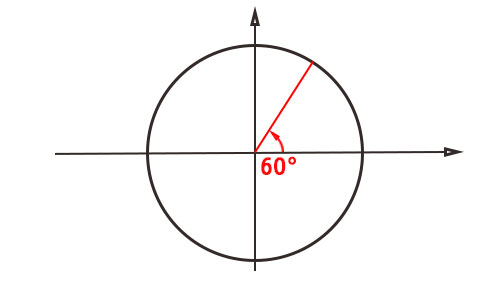
Applicando la definizione del seno e del coseno sulla figura, possiamo quindi individuare le due funzioni goniometriche che trovi qui disegnate in blu e verde.
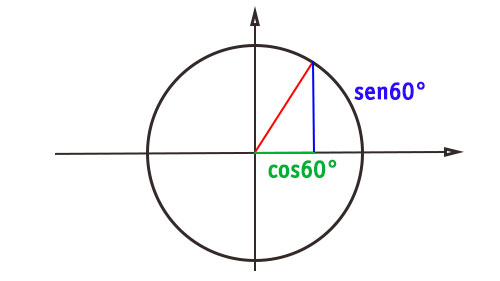
Abbiamo così disegnato il coseno e il seno di 60 gradi sulla circonferenza goniometrica. Per ricavarne il valore, basta applicare il teorema di Pitagora al triangolo che si è formato. Possiamo quindi scrivere che:
sen²60°+cos²60°=1
In realtà il triangolo in figura non è un semplice triangolo rettangolo, ma ha gli angolo di 30, 60 e 90°. Questo implica che il cateto minore è pari a metà dell’ipotenusa. Poiché quest’ultima è proprio il raggio che è pari a 1 (per definizione di circonferenza goniometrica), allora il cateto minore è 1/2. Quindi il coseno di 60° è 1/2. Per ricavare il seno di 60, basta fare sostituire quindi:
sen²60°+(1/2)²=1
sen²60°=1-1/4=3/4
A questo punto applichiamo la radice quadrata al primo e al secondo membro dell’equazione per eliminare il quadrato.
sen60°=(rad3)/2
Come ricordarlo in maniera semplice.
Hai visto quanto è stato facile ricavare il seno di 60°? Ovviamente non possiamo metterci a fare la dimostrazione ogni volta che ci vengono chiesti i valori delle funzioni goniometriche. E’ necessario impararle comunque a memoria, così da avere la risposta pronta durante le interrogazioni.
Non preoccuparti però, noi abbiamo un metodo semplice per ricordarli tutti! Gli angoli più ricorrenti sono 0°, 30°, 45°, 60° e 90°. Quelli successivi si possono ricavare con le regole degli archi associati. Quindi concentriamoci su questi primi 5 e consideriamo che:
- seno e coseno di 45° sono uguali e l’unico valore da ricordare è √2/2;
- l’angolo di 0 e 90° hanno valori di seno e coseno semplici, come 0 e 1, quindi non ci sono radici;
A questo punto non ci resta che ricordare gli angoli di 30° e 60°. Per ricavare istantaneamente quanto vale il seno di 60°, immagina la circonferenza goniometrica e i due segmenti formati da seno e coseno. Uno è più lungo dell’altro, in particolare il seno è maggiore del coseno. Per cui, visto che i valori da ricordare sono rad3/2 (circa 0,86) e 1/2 (pari a 0,5), allora il seno è (rad3)/2.