La funzione seno è una funzione trigonometrica esprimibile attraverso la relazione y=senx. Come per la funzione coseno, è definita per tutto l’insieme dei numeri reali ed è periodica. Attraverso l’analisi della funzione seno si ottiene una curva chiamata sinusoide.
![]()
All’interno di questa lezione vedremo com’è fatta e quali sono le caratteristiche della funzione seno, analizzandone dominio, grafico, punti di intersezione ed eventuali simmetrie. Vedremo quindi assieme uno studio della funzione seno completo senza però usare limiti e derivate come si fa invece nel programma di analisi.
Grafico della funzione seno
Nelle precedenti lezioni abbiamo visto quali sono i valori di seno e coseno. Abbiamo visto che conviene eseguire uno studio nell’intervallo che va da 0 a 360°, perché successivamente avremmo delle ripetizioni (l’angolo di 400° ad esempio non è altro che l’angolo di 60°, quindi è inutile studiarlo due volte).
Si parte disegnando una tabella in cui riporto i 4 valori del seno degli angoli di 0°, 90°, 180°, 270°, 360°.
| Angolo (x) | y=senx |
| 0 | 0 |
| 90° (π/2) | 1 |
| 180° (π) | 0 |
| 270° (3/2π) | -1 |
| 360° (2π) | 0 |
Per ottenere il grafico della funzione seno y=senx, ci disegniamo gli assi cartesiani e poi andiamo ad inserire i valori delle x e delle y così come li abbiamo ricavati. Sull’asse delle ascisse sono cioè riportati i valori degli angoli noti e su quello delle ordinate il risultato del seno applicato a quell’angolo.
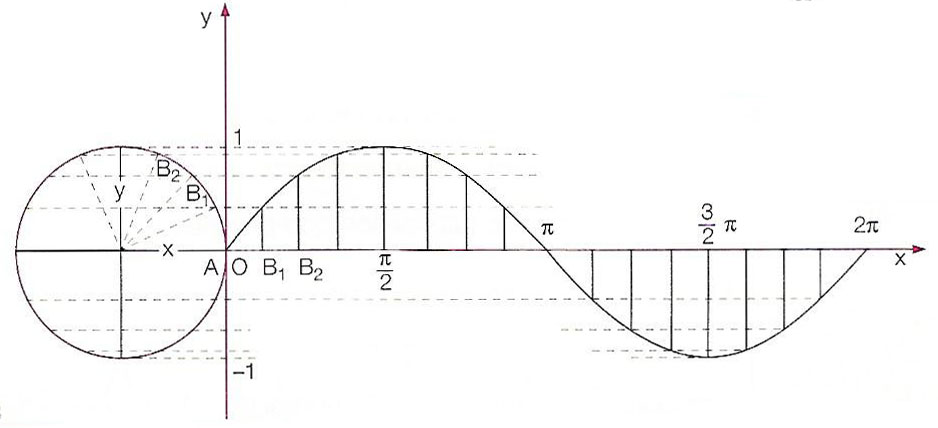
Sinusoide
La curva che si ottiene riportando sugli assi cartesiani i valori della funzione seno nell’intervallo da 0° e 360° si chiama sinusoide. Non è altro quindi che la rappresentazione grafica della funzione seno e sarà fondamentale per chi studierà in fisica il moto armonico e la natura delle onde nei programmi più avanzati.
La funzione seno è periodica
Analizzando il grafico ottenuto si può notare che quando la x=0 e quando x=2π, la y è la stessa, cioè la funzione assume gli stessi valori. Questo significa che la funzione seno è periodica con periodo pari a 2π, cioè si ripete in maniera ciclica ogni 360° assumendo sempre gli stessi valori.
Andando a considerare anche i valori che si ripetono prima di 0° e dopo 360°, possiamo ottenere il grafico della sinusoide estesa.
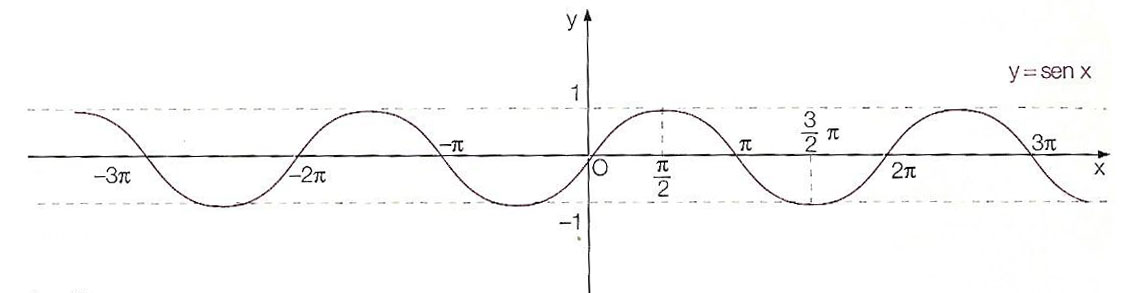
Dominio della funzione seno
Prova a rispondere a questa domanda osservando la sinusoide: la curva ha delle interruzioni oppure se dovessi disegnarla non staccheresti mai la penna dal foglio? E’ evidente che non ci sono interruzione, per cui la funzione seno è continua in tutto l’intervallo dei numeri reali.
Quindi alla domanda: quale dominio ha la funzione seno? La risposta è tutto R o, per essere più precisi nel linguaggio matematico: ∀x∈R
Codominio della funzione seno
Essendo la funzione seno invertibile, il codominio diventa dominio della funzione seno inversa (cioè la sinusoide). Proprio per questa ragione può essere chiesto dai docenti anche il codominio. Quest’ultimo non è altro che la variazione del grafico in senso verticale. La sinusoide, come puoi vedere dal grafico, è sempre compreso tra la retta y=-1 e y=+1.
Quindi il codominio è l’intervallo chiuso [-1;+1], dove i valori -1 e +1 sono compresi.
La funzione seno è simmetrica?
Altra osservazione proseguendo l’analisi della funzione seno: immagine di dividere il grafico in due zone, quella a sinistra e quella a destra dell’asse delle ordinate (y). Puoi facilmente osservare che sono praticamente identiche ma specchiate. Cioè ciò che a destra sta sopra, a sinistra sta sotto. Questo significa che c’è una simmetria rispetto all’origine degli assi.
Possiamo quindi dire che la funzione seno è dispari. Dal punto di vista matematico, ciò si può esprimere come:
f(x)=-f(-x)
cioè
sen(x)=-sen(-x)
Ad esempio
- il seno di 60 gradi sen(60°)=+1/2
- -sen(-60°)=-sen(360-60)=-sen(300°)=-(-1/2)=+1/2
Intersezione con gli assi
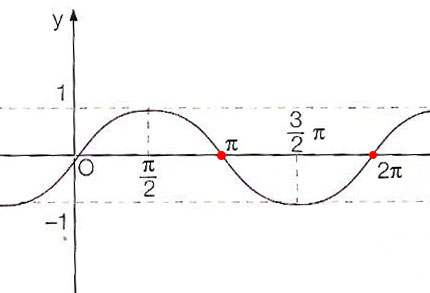
Come puoi vedere dal grafico della sinusoide, ci sono dei punti in cui la curva si interseca con l’asse delle ascisse. In particolare questi due punti hanno x=π e x=2π. Questo significa che quando gli angoli valgono 180° e 360° il seno diventa 0.
Quindi i due punti di intersezione che sul grafico abbiamo disegnato in rosso sono i punti P1(π;0) e P2(2π;0). Per determinare matematicamente questi due punti dobbiamo applicare il metodo visto con il calcolo dellintersezione tra due rette (la regola si applica per l’intersezione di due generiche curve, quindi anche della sinusoide)
Altri spunti per gli esercizi
Una volta capite le caratteristiche della funzione seno, possiamo fare qualche esercizio su grafici un po’ più complessi.
Molto spesso negli esercizi vengono chieste delle funzioni meno elementari della cosinusoide. Capita quindi di dover studiare la funzione coseno al quadrato o la funzione cos2x o ancora la funzione coseno in valore assoluto. In base a quanto detto fino ad ora è possibile dedurre il grafico di altre funzioni del coseno.
Esercizio 1
Proviamo a disegnare il grafico della funzione seno di 2x → y=sen2x
Il grafico di y=sen2x si ottiene dal grafico di y=senx mediante la contrazione di rapporti h=1/2 e k=1. In parole povere, si impone x’=2x e y’=y. Quindi ogni punto della funzione seno viene trasformata in un punto di coordinate (x’,y’).
Ricordiamo che una contrazione è una trasformazione del piano che associa ad un punto P(x,y) un punto P'(x’,y’) tale che:
x’=hx
y’=ky
con |k|≤1 e |h|≤1. Si parla di dilatazione, invece, quando |k|≥1 e |h|≥1.
Si può così costruire il grafico della funzione seno di 2x
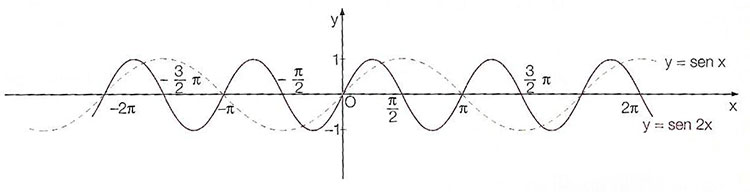
In alternativa, senza ricorrere a contrazioni e dilatazioni, semplicemente possiamo costruirci una tabella con i valori degli angoli nella prima colonna. Nella seconda ci saranno i valori della funzione seno 2x. Li si posizione sul grafico e si ottiene la sinusoide riferita a y=sen2x.
| Angolo (x) | y=sen|2x| |
| 0 | y=sen(2·0)=0 |
| 45° (π/4) | y=sen(2·π/4)=sen(π/2)=1 |
| 90° (π/2) | y=sen(π)=0 |
| 135° (3/4π) | y=sen(2·3/4π)=sen(3/2π)=-1 |
| 180° (π) | y=sen(π·2)=0 |
Si nota che il coefficiente che, considerato y=sen(k·x), il valore k provoca una contrazione della curva. Aumentano cioè le oscillazioni e la curva diventa più fitta. Si dice che tra un'”onda” e l’altra diminuisce l‘ampiezza.
Esercizio 2
Tracciare il grafico della funzione seno in valore assoluto → y=sen|x|-1
Il grafico di y=sen|x|-1 si ottiene dal grafico di y=sen|x|. Quest’ultimo si ottiene dal grafico della sinusoide ribaltando attorno all’asse delle y le parti di tale grafico che si trovano a destra dell’asse verticale. In buona sostanza si prende la curva per x>0 e la si specchia a sinistra dell’asse y.
Si ricorda infatti che il grafico di y=f|x| si ottiene dal grafico di y=f(x) semplicemente ribaltando intorno all’asse y la parte di quest’ultimo grafico che si trova a destra dell’asse y stesso.
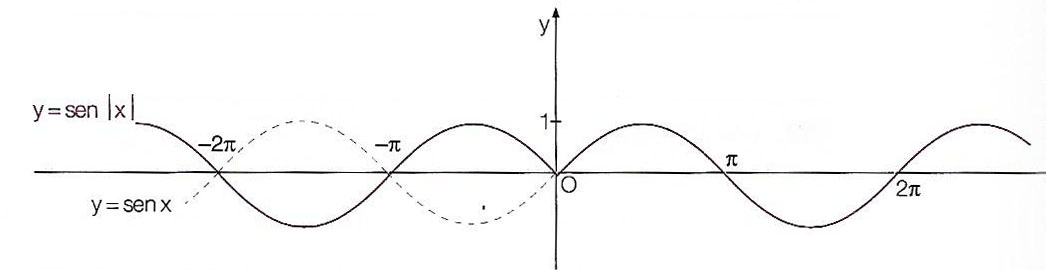
A questo punto occorre effettuare una traslazione di vettore v(0;-1). Cioè y’=y+1 e x’=x
y+1=sen|x|
y=sen|x|-1
Possiamo quindi rappresentare graficamente.
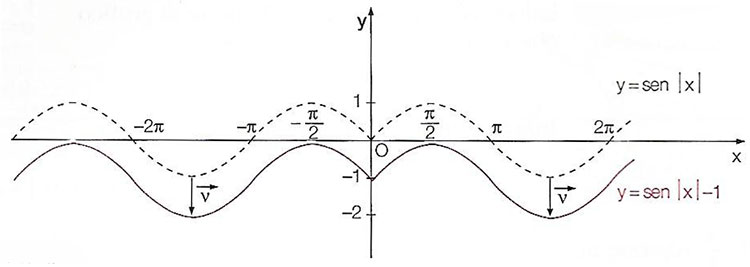
Si nota che il grafico si poteva ottenere a partire dalla funzione seno valore assoluto semplicemente traslando la sinusoide di 1 verso il basso.
Esercizio 3
Lasciamo a te a casa lo svolgimento dello stesso tipo di esercizio ma con la funzione seno al quadrato. Quindi prova a disegnare y=sen²x.