Formule di duplicazione, dimostrazione ed esercizi svolti

Le formule di duplicazione sono formule trigonometriche che permettono di ricavare i valori di seno, coseno, tangente e cotangente del doppio di un angolo. Si incontrano spesso non solo nelle equazioni goniometriche ma anche nei programmi di matematica più avanzati. In questa lezione vedremo non solo quali sono le formule duplicazione ma anche come si dimostrano.

Nell’ultima parte della lezione ci dedicheremo a degli esempi svolti e commentati con il risultato finale. Per testare le proprie abilità sono stati inseriti anche alcuni esercizi sulle formule di duplicazione da risolvere a casa. Iniziamo subito…

Formule di duplicazione tabella

In questa tabella trovi il formulario completo con tutte le formule di duplicazione del seno, coseno, tangente e cotangente. In seguito troverai poi tutte le dimostrazioni.

Formula di duplicazione del seno

Formula di duplicazione del coseno

Formula di duplicazione della tangente

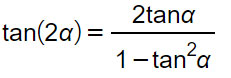
Formule di duplicazione della cotangente

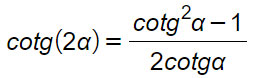
Un consiglio per non sbagliare

Ricordati che sen2a è diverso da 2sena. Infatti tutto ciò che è all’interno dell’argomento del seno o del coseno non può essere portato fuori in maniera così semplice. Per rendertene conto basta che provi a fare il calcolo con a=30°.

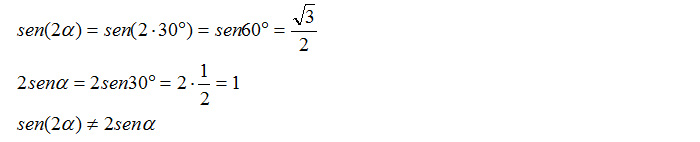
Approfondimenti: quanto vale il seno di 60°

Dimostrazione delle formule di duplicazione

Dimostrazione della formula di duplicazione del seno

Si parte dalle formule di addizione e sottrazione. In particolare si sommano due angoli uguali.

Dimostrazione della formula di duplicazione del coseno

L’unica differenza con quella del seno sta nel fatto che in questo caso bisogna applicare la formula di addizione del coseno.

In questo caso possiamo notare che è possibile scrivere la formula di duplicazione del coseno in 3 modi equivalenti. Infatti, ricordando le relazioni fondamentali della trigonometria, vale:

Possiamo ricavare il seno e il coseno e sostituirle nella formula di duplicazione del coseno:

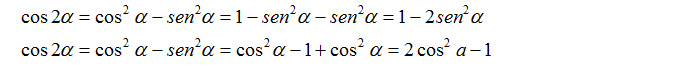
Abbiamo così trovato tre modi diversi per esprimere le formule di duplicazione del coseno, tutta valide e che possiamo utilizzare a nostro piacimento a seconda della necessità e dell’esercizio da risolvere.

Dimostrazione della formula di duplicazione della tangente

Per dimostrare le formule di duplicazione della tangente, facciamo riferimento a quella che abbiamo considerato la dimostrazione della tangente di un angolo.

Inseriamo le formule di seno e coseno calcolate in precedenza all’interno della formula della tangente per ottenere:

Proviamo a questo punto a dividere sia il numeratore che il denominatore della frazione per il coseno al quadrato dell’angolo. In questo modo otteniamo:

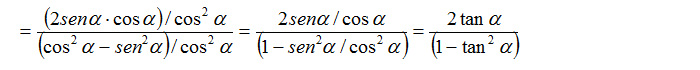
Dimostrazione della formula di duplicazione della cotangente

Dimostrare la formula di duplicazione della cotangente è molto semplice, soprattutto se avete seguito la dimostrazione della formula di duplicazione della tangente.

Per questo motivo potete provare a farlo da soli ricordando che questa volta l’equazione da cui bisogna partire è cotg2a=cos2a/sen2a.

Esercizi svolti sulle formule di duplicazione

• sen(2α)-cosα=0
  Applichiamo la formula di duplicazione del seno all’esercizio.

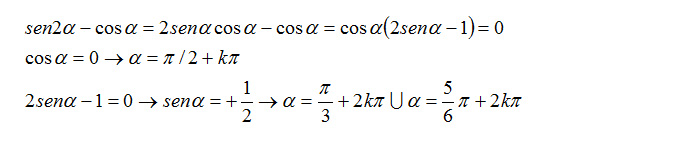
E’ stato sufficiente un raccoglimento a fattor comune e la risoluzione di due semplici equazioni trigonometriche.

Esercizi da risolvere

Prova ora a risolvere gli esercizi da solo. Ovviamente se ci sono problemi con la lezione o non riesci a svolgere i compiti di trigonometria assegnati a scuola, contattaci. Saremo lieti di aiutarti.

• sen2a=1
• cos2a=1