Qual è la definizione di funzione matematica? Si tratta di uno degli argomenti più importanti ma allo stesso tempo difficili da capire per gli studenti. Implica alcuni concetti e definizioni (come il dominio) che saranno molto utili negli esercizi di analisi.
Per capire questa lezione è importante avere alcune nozioni che riguardano la teoria egli insiemi. Infatti per parlare di definizioni di funzioni reali, dovremo valutare le alcune condizioni che riguardano due insiemi particolari. Entriamo però subito nel vivo della lezione
Definizioni di funzioni
Iniziamo subito questa lezione dandoti la definizione di funzione matematica che trovi in genere su tutti i libri di testo:
Si definisce funzione matematica quella legge che associa ad ogni elemento di un insieme A uno ed un solo elemento dell’insieme B.
Per capire che cos’è una funzione iniziamo disegnando due insiemi generici, A e B, non vuoti, cioè che al loro interno sono presenti degli elementi.
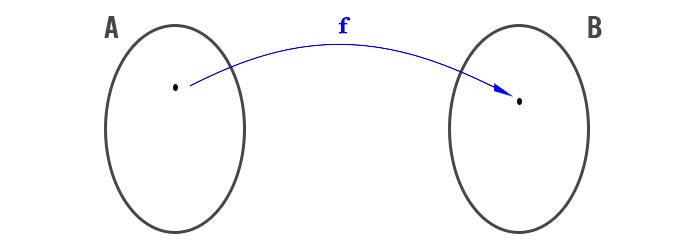
Che cos’è una funzione?
Come puoi vedere l’elemento dell’insieme A viene collegato con l’elemento dell’insieme B con una freccina che si chiama f. E’ proprio questo il concetto di funzione. Detto quindi in parole povere da un insieme A (che sarà il dominio, cioè l’insieme delle x), attraverso un oggetto matematico (appunto la funzione) arriviamo all’insieme B (che sarà l’insieme delle y).
Scritto in maniera matematica:
f:A → B
Che significa? Applicando una f all’insieme A arriviamo in B.
Un altro modo per indicare la funzione in matematica è f(a)=b dove a e b sono i generici elementi dell’insieme A e B rispettivamente. Molto spesso troverai infatti scritto sui libri: data la funzione y=f(x).
Ma che cos’è una funzione? La definizione l’abbiamo capita, ma nella pratica chi è f? E’ una qualsiasi operazione o operatore matematico applicato alla x. Ecco alcuni esempi:
- x+1 è una funzione perché dato un valore di x, f ci dice di aggiungere +1 per ottenere la y.
- x² è una funzione perché dato un valore di x, la f ci dice di farne la radice quadrata per ottenere la y.
- sin x anche il seno è una funzione perché data una x, la f ci dice di applicare il seno per ottenere la y.
Che cosa sono il dominio e il codominio
Accanto alla definizione di funzione, ci sono due concetti importanti da conoscere e che andranno applicati negli esercizi di analisi e negli studi di funzione: dominio e codominio. Che cosa sono?
- L’elemento dell’insieme B (il puntino a destra) si definisce immagine dell’elemento nell’insieme A (il puntino a sinistra)
- L’elemento dell’insieme A si definisce controimmagine dell’elemento in B
- L’insieme A si definisce dominio della funzione f e si indica con la lettera D
- L’insieme B si definisce codominio della funzione f e si indica con la lettera C
Esempio: è una funzione
Vediamolo più facilmente con un esempio. Ti ricordi come si disegna una retta? Molto brevemente assegnavamo un valore alla x a nostra scelta e calcolavamo la y di conseguenza.
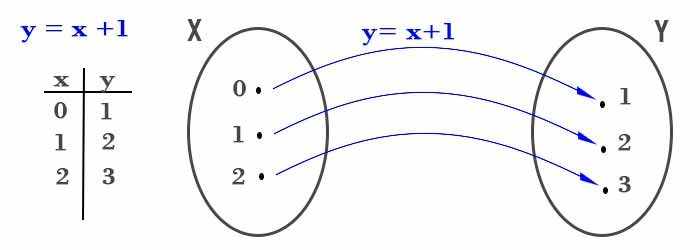
y=x+1 è una funzione, nello specifico è l’equazione di una retta. Ad ogni valore di x corrisponde uno ed un solo valore di y, quindi è rispettata la definizione di funzione matematica.
Esempio: NON è una funzione
La circonferenza non è una funzione matematica. Ti ricordi l’equazione della circonferenza? Vediamo l’esempio…
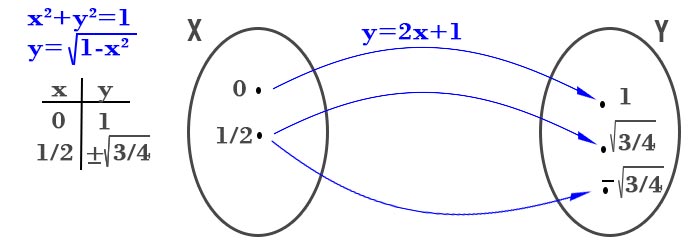
Come puoi vedere in corrispondenza del valore 1/2 della x sono associati 2 valori alla y. Questo significa che la circonferenza goniometrica rappresentata dalla formula non è una funzione matematica.
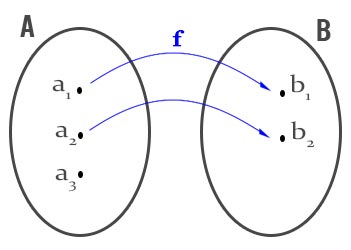
NON è una funzione
Dalla definizione di funzione è possibile anche fare un’importante osservazione: tutti gli elementi dell’insieme A devono essere collegati ad uno e un solo elemento di B. Questo significa che se c’è qualche punto di B non collegato allora non si parla di funzione ma di una semplice relazione tra gli elementi degli insiemi.
Nella figura a destra, ad esempio puoi vedere che l’elemento a3 non è associato in alcun modo con alcun elemento dell’insieme B. f quindi non una funzione.
Definizione di funzione, esercizi
Capito quindi che cos’è una funzione, consideriamo le seguenti equazioni e stabiliamo se esse rappresentano funzioni matematica.
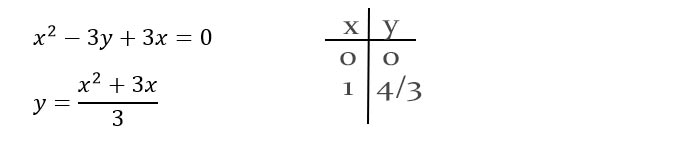
A partire dalla traccia abbiamo ricavato la y e poi verificato sul grafico la corrispondenza tra dominio e codominio. Questo primo esercizio è certamente una funzione perché per ogni valore di x che noi andiamo ad assegnare, esiste uno e un solo valore della y, proprio come dice la definizione di funzione. Il secondo esercizio invece è leggermente diverso.
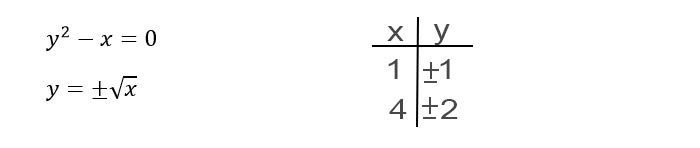
Una volta esplicitata la y in funzione della x, mi rendo subito conto che assegnando alla variabile indipendente (cioè alla x) un valore arbitrario, trovo due valori della variabile dipendente, cioè la y.
Nelle prossime lezioni tratteremo la definizione di funzione iniettiva, suriettiva e biettiva e vedremo che cos’è una funzione crescente o decrescente. Se intanto hai dei dubbi puoi usare il modulo dei contatti e scriverci una mail con i tuoi problemi, altrimenti puoi usare la chat in basso nello schermo per parlare live con i nostri docenti.
Buonasera, Io cercavo la spiegazione di funzione e credo di averla trovata. Sono uno studente attempato che dopo molti anni ha deciso di riprendere gli studi iscrivendomi a Scienze politiche quindi lascio immaginare le difficoltà. Spero di trovare in questo sito documenti o lezioni che mi aiutino sia nella preparazione all’esame di economia politica che a quello di statistica che preparerò subito dopo.
Grazie dell’aiuto
Gianfranco De Benedictis
Buongiorno Gianfranco,
se possiamo aiutarti in qualche modo non esitare a contattarci. Buono studio
Gentile Dott. Calicchio,
Anche io, come Gianfranco, sto facendo un ripasso…
Non capisco, però, perché – nell’esempio della equazione della retta – ad un valore di x pari a 2, y non valga 5…
Grazie per il chiarimento
Cordialità
Grazia
Gentile Dott. Calicchio,
mi scuso, ma ho dimenticato di farle i complimenti per la chiarezza espositiva…
Grazie di cuore
Grazia
Buongiorno Grazia,
sulla traccia c’era un refuso che è stato prontamente corretto. Grazie per la segnalazione e per l’apprezzamento verso la qualità delle lezioni. Buono studio