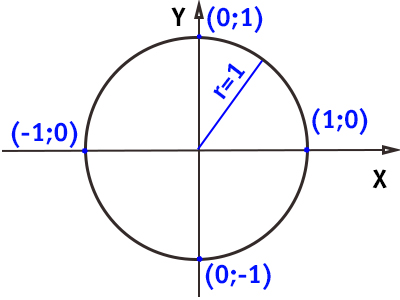
La circonferenza goniometrica è una circonferenza con raggio unitario e centro nell’origine degli assi cartesiani. Grazie a questa figura si riescono a definire seno e coseno, assieme alle altre funzioni goniometriche.
In questa lezione vedremo che cos’è, come si disegna e a che cosa serve la circonferenza goniometrica. Analizzeremo inoltre assieme quelli che saranno i punti più importanti da fissare su questa figura e che spesso richiameremo nelle prossime lezioni di trigonometria.
Un breve ripasso consigliato: circonferenza definizione elementare
Definizione di circonferenza goniometrica
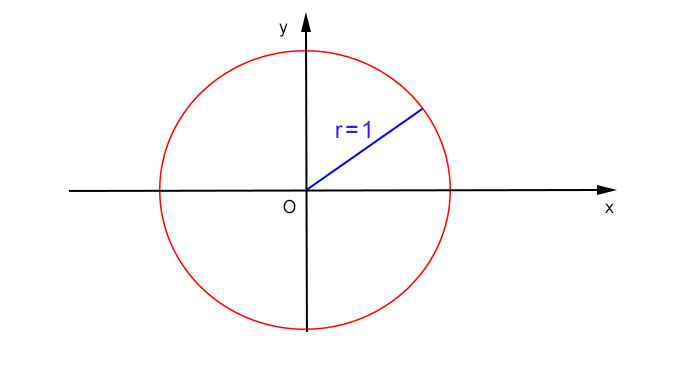
E’ la circonferenza di raggio unitario con centro nell’origine
Vedi quanto è semplice la definizione? Però in base a questo semplice cerchio goniometrico praticamente tutto il programma di geometria analitica. Ti ricordi qual è l’equazione di una circonferenza noto il centro e il raggio?
![]()
dove α e β sono ascissa e ordinata del centro. Poiché abbiamo detto per definizione che la circonferenza ha centro nell’origine, queste due coordinate cartesiane sono pari a 0. Tenendo conto anche che il raggio è pari a 1, l’equazione della circonferenza può riscriversi come:
![]()
Siamo così arrivati all’equazione della circonferenza goniometrica. E’ proprio da questa formula che, nelle prossime lezioni, andremo a scrivere le relazioni fondamentali della goniometria.
Come si disegna
Disegnare la circonferenza goniometrica è un procedimento molto semplice che puoi fare tranquillamente anche su un normale foglio a quadretti. Proviamo a farlo insieme:
- Tracciate un piano cartesiano con x, asse delle ascisse, e y, asse delle ordinate. Segniamo il loro punto di intersezione in O cioè l’origine.
- Prendete un compasso e scegliete la dimensione del raggio aprendolo per esempio di 5 cm. Tracciate la circonferenza goniometrica puntando nell’origine degli assi, cioè il punto O.

Puoi vedere dalla figura che il raggio forma con l’asse delle x un angolo, che viene definito in matematica angolo orientato. Questo perché la sua misura dipende dal verso di percorrenza. L’angolo sarà positivo se il raggio si muove in senso antiorario (quindi va verso l’alto partendo dall’asse x), sarà negativo se si muove in senso orario (quindi va verso il basso partendo dall’asse x).
Gli angoli delle circonferenza goniometrica più importanti
Da 0 a 360° sono davvero tanti gli angoli possibili che il raggio della circonferenza goniometrica può individuare con l’asse delle ascisse. Tuttavia ce ne sono alcuni, detti anche angoli noti, che ci ritroveremo spesso in esercizi e problemi. Vale quindi la pena iniziare a capire quali siano. Di seguito vengono elencati con la loro misura in gradi e in radianti. Per le trasformazioni da un sistema di misura all’altro consulta la nostra lezione sulla conversione gradi radianti.
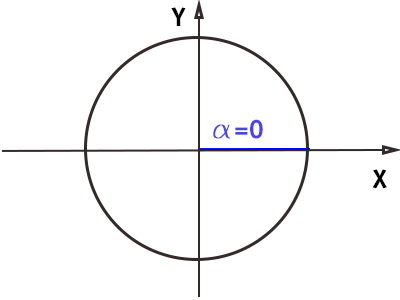
Angolo di 0°
E’ il primo che si individua quando il raggio della circonferenza goniometrica non ha neanche iniziato a muoversi.
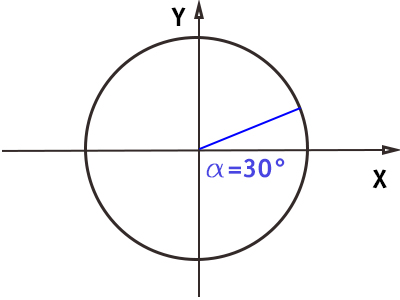
Angolo di 30° (π/6)
Il raggio ha iniziato a muoversi e si ferma poco prima della bisettrice del primo e terzo quadrante.
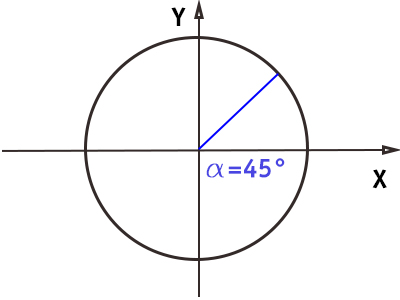
Angolo di 45° (π/4)
Il raggio della circonferenza goniometrica è arrivato a metà strada tra 0° e 90°
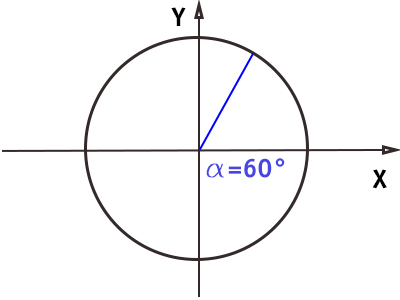
Angolo di 60° (π/3)
E’ il valore speculare sulla circonferenza goniometrica dell’angolo di 30° e, come vedremo nelle prossime lezioni, è a lui molto simile per alcuni valori che assumerà con le funzioni trigonometriche.
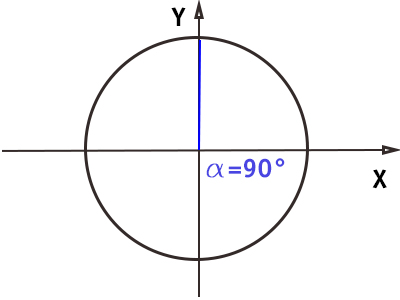
Angolo di 90° (π/2)
Il raggio ha raggiunto l’asse delle ordinate della circonferenza goniometrica. Siamo arrivati all’angolo retto.
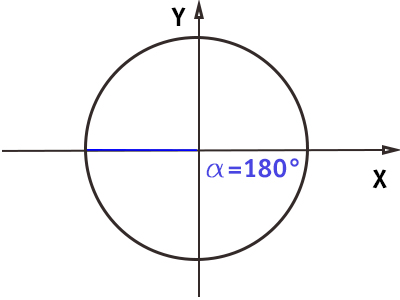
Angolo di 180° (π)
E’ l’angolo piatto. Continuando a spostarsi lungo la circonferenza goniometrica, il raggio ha toccato di nuovo l’asse delle ascisse.
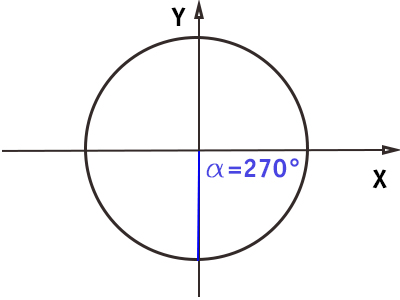
Angolo di 270° (3/2 π)
E’ l’angolo sulla circonferenza goniometrica speculare all’angolo retto.
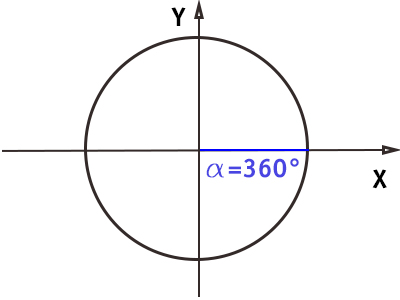
Angolo di 360° (2 π)
Il raggio ha percorso tutta la circonferenza unitaria ed è tornato al punto di partenza. Infatti tutto ciò che riguarda l’angolo di 360° lo si può dire ugualmente all’angolo di 0°.
A cosa serve la circonferenza goniometrica?
Abbiamo detto che questa figura geometrica particolare servirà a definire i concetti di seno, coseno, tangente e cotangente. In realtà la sua utilità non si ferma qui.
Da quanto abbiamo detto fino ad ora, lo studio sulla circonferenza trigonometrica si interessa di tutti gli angoli che vanno da 0 a 360°, quindi scritto in maniera matematica:
0≤α≤2π
Che cosa succede però quando l’angolo supera i 360°, cioè i due pi greco? Come ci si comporta con un angolo di 400° gradi ad esempio? Sena andare a complicarsi la vita per capire come trasformarli in radianti e senza affrontare le trattazioni teoriche di cui si è tanto discusso nei secoli ragioniamo in maniera semplice.
Quando il raggio supera i 360° inizia a percorrere da capo la circonferenza goniometrica percorrendo di fatto una strada già percorsa in precedenza. Per cui non fa altro che ripetere quanto già fatto prima. Per questa ragione ha senso ricondurre tutti gli angoli maggiori di 360° all’interno dell’intervallo 0-360°. Come? Basta sottrarre 360°!!
Ad esempio un angolo di 700°: 700-360=340°1507
Conclusioni
Abbiamo così concluso questa che consideriamo come una delle lezioni introduttive del programma di geometria goniometrica. A partire dalle prossime lezioni potremo definire i concetti di funzioni goniometriche (seno, coseno, tangente, …).
Nel frattempo, se ti è tutto chiaro e se la lezione ti è stata utile, lascia un commento in basso. Ci aiuterai a proseguire nella stesura sempre di nuove lezioni e a migliorare la qualità delle lezioni. Buono studio 😉
Professor CALICCHIO,
i suoi studenti hanno ragione riguardo le sue lezioni e la chiarezza con cui trasmette tutta la sua sapienza.
Complimenti da una persona che, dopo svariati anni, ha dovuto riprendere in mano i libri ed alcune tra le vecchie lezioni incomprese, sia di scuola superiore che universitarie, e grazie a Lei, ora apprese con semplicità.
Spero che vada avanti nel suo meraviglioso percorso e modo di elargire la conoscenza ad altri.
Cordialmente
Maria.