Le formule trigonometriche sono dette anche formule goniometriche e rappresentano forse l’argomento più impegnativo del programma di trigonometria. Ci sono tante formule, non facili da imparare.
Abbiamo quindi raccolto in un’unica pagina il formulario completo delle formule di trigonometria. Partiremo dalla relazione fondamentale della trigonometria per passare poi alle formule di duplicazione, bisezione, parametriche per seno e coseno, prostaferesi, Werner, eccetera…
In questa lezione vedremo solo le formule, mentre per le dimostrazioni delle formule trigonometriche ci sarà una lezione di approfondimento per ciascuna di esse. Abbiamo deciso di creare questo formulario per semplificare la vita allo studente, consapevoli del fatto che non è facile ricordarle tutte a memoria, per cui è meglio averle sempre a portata di mano in una tabella con un formulario completo. Partiamo subito con questa rassegna completa delle principali relazioni trigonometriche.
Formule trigonometriche principali
Relazione fondamentale della trigonometria
Iniziamo questo formulario di trigonometria con la primissima relazione che si studia in questo ramo della matematica. Viene detta anche identità o relazione fondamentale della goniometria. Permette di ricavare il seno a partire dal coseno e viceversa. Ti consigliamo di ricordarla perché viene molto utilizzata negli esercizi ed è piuttosto semplice.
sen²α+cos²α=1
Per ricavare seno e coseno basta ricorrere alle due formule inverse:
- sen²α=1-cos²α
- cos²α=1-sen²α
Formule trigonometriche sugli archi associati
Gli archi associati sono utili per poter calcolare i valori delle varie funzioni goniometriche per tutti gli angoli a partire da seno e coseno di angoli noti. Ad esempio, avendo a disposizione il seno di 60 gradi possiamo calcolare il coseno anche di 120°, di 150°, eccetera…
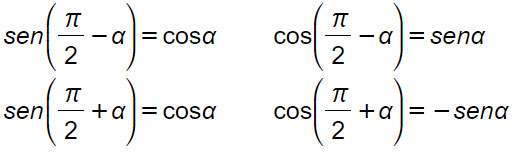
Come ricordarle: quando c’è l’angolo di 90° (quindi π/2) ricorda che bisogna invertire seno e coseno. Il coseno con α+π/2 assumerà un segno meno perché ci troviamo nel II quadrante. (Leggi anche: quali sono i segni dei quadranti del piano cartesiano)

Come ricordarle: quando c’è l’angolo di 180° si conservano seno e coseno. Con il segno “meno” siamo nel II quadrante per cui il coseno assume segno negativo. Con il segno “più” sia il seno che il coseno diventano negativi.
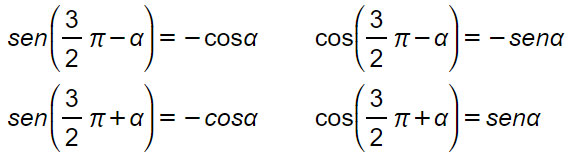
Come ricordarle: quando c’è l’angolo da 270°, si ripete quello che accadeva con le formule trigonometriche riferita a 90°. Quindi si invertono seno e coseno. Attenzione ai segni perché siamo nel III e IV quadrante.
![]()
Come ricordarle: in questo caso abbiamo l’angolo negativo (che è sinonimo di 360-a). Seno e coseno si conservano solo che il seno è negativo e il coseno è positivo perché siamo nel IV quadrante.
Formule di addizione e sottrazione
Le formule di addizione e sottrazione servono per ricavare i valori di seno e coseno semplicemente sommando due angoli. Se ad esempio dovesse esserci chiesto di calcolare il seno di 75°, che non è un angolo noto, possiamo calcolarlo considerando 75° come la somma di 30° + 45°, che sono due angoli noti.
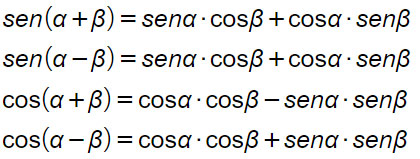
Note: alcuni testi riportano anche le formule goniometriche di addizione e sottrazione per la tangente. Tuttavia vengono utilizzate molto raramente. Abbiamo preferito non riportartele, anche perché se dovessi trovarti ad utilizzare un somma o differenza riferita alla tangente, calcola seno e coseno e poi li dividi. (Ricorda che tgα=senα/cosα, vedi la lezione sulla tangente di un angolo).
Formule di duplicazione
Le formule di duplicazione servono per calcolare la funzione goniometrica riferita al doppio dell’angolo.
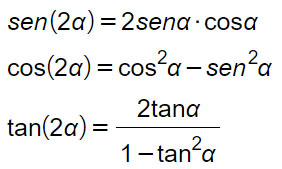
Formule di bisezione
Le formule di bisezione servono per calcolare la funzione goniometrica riferita alla metà dell’angolo.
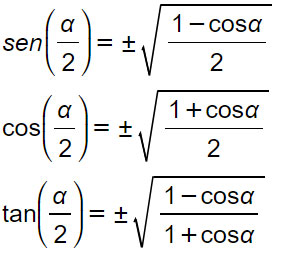
Formule parametriche
Le formule parametriche prevedono un cambio di variabile. Al posto dell’angolo α si sostituisce il parametro t. Il loro uso è di fondamentale importanza per lo svolgimento delle equazioni goniometriche. Vengono anche utilizzate in programmi di matematica più avanzati, come nello studio degli integrali.
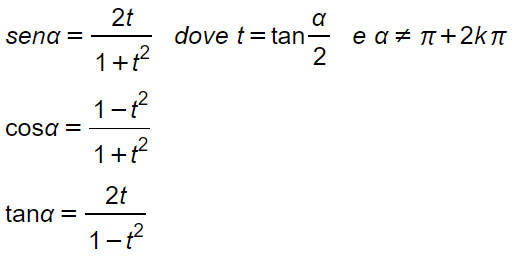
Formule di Prostaferesi
Le formule di Prostaferesi permettono di risolvere quegli esercizi in cui compaiono le somme di seni e coseni di angoli diversi. Attraverso queste formule trigonometriche la somma viene trasformata in un prodotto rendendo più agevoli i calcoli.

Formule di Werner
Si tratta di formule goniometriche particolarmente utili negli esercizi in cui l’argomento di seno e coseno è moltiplicato per un numero. Ad esempio per calcolare sen7x·sen9x occorre utilizzare le formule di Werner.
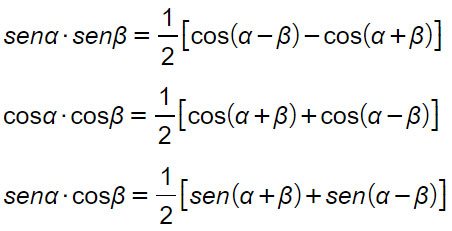
Conclusioni
In questo formulario di trigonometria abbiamo dato spazio esclusivamente alle formule, con alcuni utili suggerimenti per memorizzarle meglio. Le formule trigonometriche sui triangoli rettangoli verranno trattati in una lezione separata, perché meritano più spazio rispetto ad un semplice formulario.
Per dubbi o chiarimenti, lascia un commento qui in basso e il nostro staff risponderà nel minor tempo possibile.