Iniziamo subito con la definizione di funzione invertibile, tanto importante nel programma di analisi.Una funzione invertibile è tale se si può definire una nuova funzione f-1 detta funzione inversa.
Definizione di funzione invertibile
data una funzione f:A -> B, se ad ogni y=f(x) appartenente a B corrisponde un solo x appartenente ad A viene definita una nuova funzione f-1 detta funzione inversa di f.
f-1:B -> A con x=f-1(y)
Probabilmente ci hai capito ben poco. Non scoraggiarti, è normale. In questa lezione cercheremo di semplificarti al massimo tutti i concetti di matematica da imparare. Vediamo di dare una spiegazione più facile da capire.
Ti ricordi la definizione di funzione che abbiamo visto nelle lezioni precedenti? La funzione è una relazione che lega gli elementi dell’insieme A con quelli dell’insieme B. Così come vedi in figura.
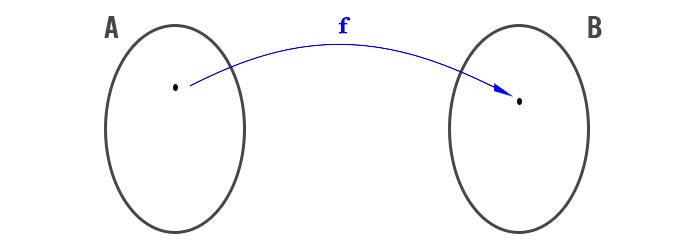
Definizione di funzione
La funzione inversa invece si ha quando la freccia blu nell’immagine parte da B e arriva ad A. Sostanzialmente nella funzione normale hai la y a sinistra e tutte le x a destra. Sfruttando le funzioni invertibili hai invece la x a sinistra e tutte le y a destra.
Esempio
Sia la nostra funzione da invertire y=x+1. Qual è la funzione inversa? Basta spostare la x a sinistra seguendo le regole delle equazioni di primo grado (come quella di cambiare il segno quando un elemento viene spostato). Il risultato è: x=y-1 ed è proprio la funzione inversa che stavamo cercando.
La domanda da porsi a questo punto è: ma tutte le funzioni sono invertibili? Quando una funzione è invertibile? Ci sono delle condizioni da rispettare, esiste una regola che mi possa aiutare a risolvere gli esercizi di matematica?
Quando una funzione è invertibile?
- Se una funzione è monotòna (cioè strettamente crescente o strettamente decrescente) allora la funzione è invertibile.
- Se l’equazione y=f(x) risolta rispetto ad x ammette una sola soluzione per qualsiasi valore di y, allora la funzione è invertibile.
Quando risolvi i tuoi esercizi, verifica che siano rispettate queste due condizioni. Sono sufficienti per definire una funzione invertibile.
Esercizi
La parte teorica è praticamente conclusa. Vediamo alcuni esercizi svolti così da verificare le nostre conoscenze.
Esempio 1
y=2x è una funzione invertibile?
Per saperlo basta ricavarci la x. L’inversa della funzione esponenziale è la funzione logaritmica, per cui ci basta fare il logaritmo in base 2 ad entrambi i membri per ottenere.
log2y=log22x che diventa x=log2y
Esiste quindi una sola soluzione rispetto alla x, per cui l’esponenziale datoci dalla traccia è una funzione invertibile. Inoltre osserviamo che il dominio della funzione f è tutto R, mentre il codominio esiste solo per valori di y>0. Nella funzione inversa (cioè quella con il logaritmo che abbiamo calcolato) il dominio e il codominio sarà le inverse rispetto a quelle calcolate per f.
Esempio 2
y=x2 è una funzione invertibile?
Per scoprirlo come nell’esercizio precedente proviamo a calcolare la x, per ottenere x= ± radice quadrata di y. In questo caso la funzione è invertibile in un intervallo dato, cioè restringendo il suo dominio. In particolare:
- per x≥0 -> x=radice di y
- per x<0 -> x= – radice di y
Esempio 3
Verifichiamo che la funzione è invertibile anche solo localmente y=x2-2x-3.
Si tratta di un’equazione di secondo grado per cui facendo il grafico otteniamo una parabola. Questa figura ha come caratteristica di essere per un tratto decrescente ed uno crescente. Poiché il vertice è V(1;-4), allora la funzione è invertibile negli intervalli (-∞;1] e [1;+∞).
Provando a ricavare la x otteniamo: x1,2=1± radicequadrata(1+3+y)=1± radicequadrata(4+y), con y≥-4
- per x≤1 -> x=1-radicequadrata(4+y)
- per x>1 -> x=1+radicequadrata(4+y)