Come si calcola l’area del trapezio isoscele? Quali formule si possono usare? E’ possibile avere alcuni esercizi svolti sul calcolo dell’area di un trapezio isoscele? – Marco
Risposta
L’area del trapezio isoscele rappresenta la misura della superficie racchiusa nel perimetro della figura. Si calcola utilizzando le classiche formule sui trapezi: base maggiore più base minore per altezza diviso due.
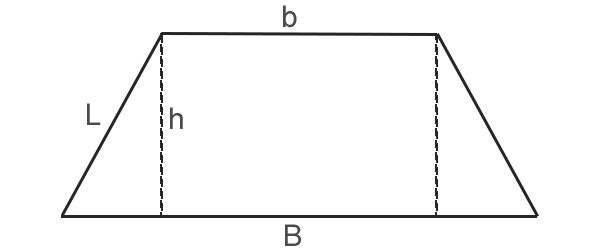
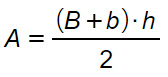
Dove B è la base maggiore, b la base minore, h l’altezza e A l’area del trapezio isoscele.
Come si calcola l’area del trapezio isoscele dato il lato obliquo?
Non sempre la traccia fornisce tutti i dati già pronti per risolvere l’esercizio. Nel caso in cui venisse data la misura del lato obliquo, dovremo sfruttare il teorema di Pitagora.
In questo modo sarà possibile determinare l’altezza o il segmento alla base del triangolo rettangolo che si forma a sinistra e a destra della figura. Vedremo comunque negli esercizi svolti, più nel dettaglio come calcolare l’area del trapezio isoscele nei casi più complessi.
Prima vediamo come si arriva alla formula con una brevissima dimostrazione grafica.
Dimostrazione formula area trapezio isoscele
Per dimostrare la formula dell’area è necessario trasformare il trapezio isoscele così come vedi in figura. Si inizia disegnando sul lato BC il punto medio M e poi il segmento DM.
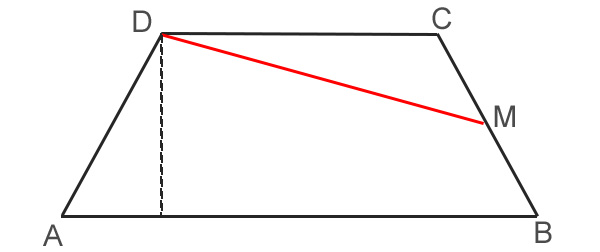
A questo punto effettuiamo una rotazione del triangolo DCM attorno al punto M così come nella figura di seguito.
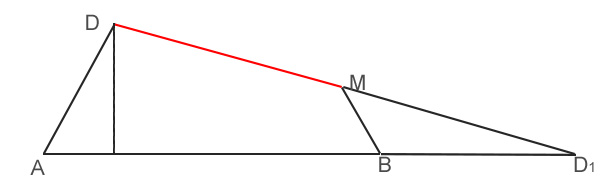
Il triangolo precedentemente indicato come DCM ora è diventato il triangolo MBD. In totale si ottiene una figura AD1D pari proprio ad un triangolo la cui area è:
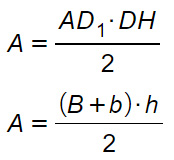
Esercizi sull’area del trapezio isoscele
Esercizio 1
In un trapezio isoscele ABCD le basi misurano rispettivamente 12 e 28 cm, mentre il lato obliquo 10 cm. Calcola l’area del trapezio isoscele e la sua altezza.
Svolgimento
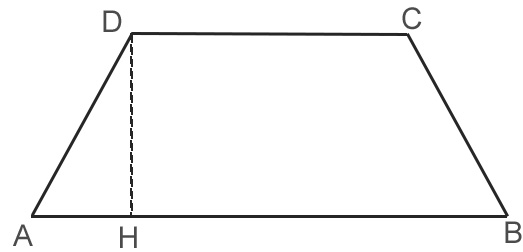
Subito dopo aver disegnato la figura, vediamo che abbiamo a disposizione le basi AB e DC, mentre serve l’altezza DH.
Possiamo calcolarla ricorrendo al teorema di Pitagora applicato al triangolo ADH, dove il lato obliquo AD è noto e possiamo ricavare il cateto AH. Come? Come la semisomma delle basi…
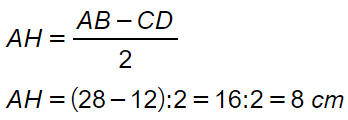
A questo punto applichiamo la formula inversa del teorema di Pitagora per determinare l’altezza.
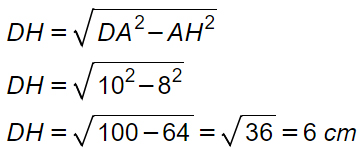
Possiamo infine calcolare l’area del trapezio isoscele con la formula:
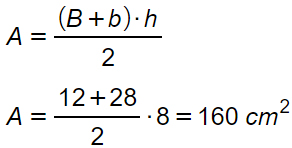
Esercizio 2
Calcolare l’area di un trapezio isoscele che ha le basi di 50 cm, 20 cm e l’altezza di 8 cm.
Svolgimento
Esercizio molto più semplice del precedente. Abbiamo tutti i dati a disposizione per applicare la formula direttamente:
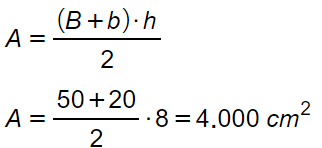
Conclusioni
Se la lezione ti è stata utile o se hai ancora dei dubbi sull’argomento, lasciaci un feedback nei commenti in basso. Il nostro staff risponderà ad ogni tua domanda nel minor tempo possibile.
Salve non ho capito perchè l’altezza e 8 e no 6 nel primo esercizio ,mi potreste spiegare .Grazie.
Buongiorno Elvira,
il segmento che misura 8 cm è AH che, come puoi notare dalla figura, è una parte della base del trapezio. L’altezza invece, calcolata con il teorema di Pitagora, misura 6 cm.