Il triangolo scaleno è un poligono avente tutti i 3 lati ed angoli diversi. Le formule che lo caratterizzano sono molto semplici: come si calcola l’area del triangolo scaleno? Come si calcola il perimetro, i lati o l’altezza?
In questa lezione vedremo tutto quello che c’è da sapere su questa figura geometrica, analizzando le formule per calcolare l’area del triangolo scaleno e tutti i suoi lati. Nella parte finale della lezione vedremo tre problemi svolti e commentati passo passo che spesso mettono in difficoltà gli studenti.
Tutte le formule triangolo scaleno
Tra i vari parametri da calcolare nei problemi, la superficie è quella che generalmente crea più dubbi. L’area del triangolo scaleno, così definito perché ha tutti i lati di lunghezza diversa, non è di immediata individuazione così come accade per il triangolo isoscele o rettangolo.
Per questa ragione abbiamo creato questa pagina di approfondimento: qui riporteremo tutti i metodi di calcolo della superficie del triangolo scaleno che possono essere utilizzati. Oltre all’area vedremo anche tutte le formule del triangolo scaleno.
Area triangolo scaleno – i due metodi da utilizzare
I metodi da utilizzare sono quelli che valgono in linea generale per tutti i tipi di triangoli.
1) Base per altezza diviso 2
La formula principale che siamo abituati ad utilizzare per i triangoli recita:
L’area di un triangolo si calcola dividendo per due il prodotto tra base ed altezza.
A=b×h:2
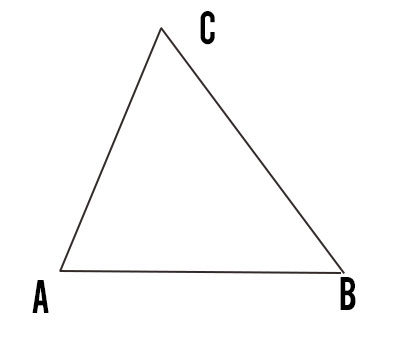
Ma qual è la base? Guardando la figura, non necessariamente si deve considerare AB come la base del triangolo, anzi. Tutti i lati possono assolvere al ruolo di base, purché l’altezza usata poi nel calcolo sia relativa a quello stesso lato. Per questa ragione possiamo scrivere le seguenti 3 formule per il calcolo dell’area triangolo scaleno:
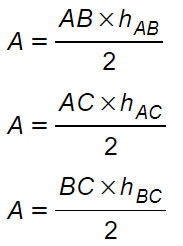
QUANDO USARLA: In questo primo metodo è ovviamente indispensabile conoscere uno dei lati, che verrà considerato come base, e l’altezza relativa allo stesso lato.
2) Formula di Erone
Il secondo metodo per calcolare l’area del triangolo scaleno è consiste nell’applicazione della formula di Erone.
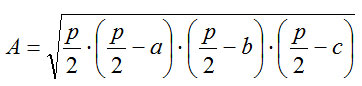
dove:
- p= perimetro;
- a,b,c = sono i tre lati del triangolo.
Quindi il primo passo è quello di calcolare il perimetro sommando i lati e poi dividerlo per due, così da ottenere il semiperimetro.
QUANDO USARLA: questa formula va usata soltanto se si hanno immediatamente disponibili le misure dei tre lati del triangolo.
Perimetro triangolo scaleno
Il perimetro misura l’estensione in lunghezza della figura e si calcola facendo la somma di tutti i lati. Quindi la formula è molto semplice:
p=AB+BC+AC
Calcolo dei lati e dell’altezza
Per avere a disposizione tutte le formule triangolo scaleno mancano la misura dei lati e dell’altezza. Si ricavano a partire dalla formula dell’area del triangolo scaleno. Abbiamo scritto una lezione proprio per tutte le formule inverse dell’area.
Triangolo scaleno, esercizi e problemi svolti
Esercizio 1
Calcolare l’area del triangolo scaleno che ha la base pari a 28,5 cm ed ha l’altezza il doppio della base.
La traccia ci fornisce indirettamente sia la base che l’altezza. Quest’ultima la calcoliamo semplicemente andando a moltiplicare la base per 2. Per cui:
h=28,5 cm × 2 = 57 cm
A questo punto possiamo usare la prima formula vista, cioè:
A=b×h:2
A=28,5 cm × 57 cm : 2= 812,25 cm²
Esercizio 2
In un triangolo l’altezza è 5/3 della base e la loro somma misura 160 cm. Calcola l’area del triangolo isoscele.
Mentre per uno studente delle scuole superiori basta semplicemente impostare un sistema di equazioni di primo grado, uno studente delle scuole medie potrebbe avere difficoltà a risolverlo. Per cui risolviamo l’esercizio ricorrendo alle unità frazionarie.
h=5/3 b
Questo vuol dire che b=3u e h=5u. In tutto sono 8u. Poiché la somma è 160 cm, vuol dire che ogni unità frazionaria sarà:
160 cm : 8 = 20 cm
Per cui
b=20×3=60 cm
h=20×5=100 cm
A questo punto possiamo calcolare l’area del triangolo scaleno con la classica formula:
A=b×h:2=60×160:2=4.800 cm²
Esercizio 3
Calcolare l’area del triangolo scaleno in cui la somma e la differenza della misura di base e altezza è 44 cm e 12 cm.
E’ un altro esercizio che generalmente mette in difficoltà gli studenti delle scuole medie. Mentre alle superiori si risolvere in meno di 30 secondi impostando un piccolo sistema di primo grado, per gli studenti delle scuole medie occorre agire diversamente. Traduciamo intanto in linguaggio matematico i dati a disposizione:
AB+CH=44 cm
AB-CH=12 cm
Essendo la differenza tra i due segmenti maggiore di zero, vuol dire che la base AB è più grande dell’altezza CH. Cioè AB>CH. Per calcolare questi due segmenti si ragiona in questo modo:
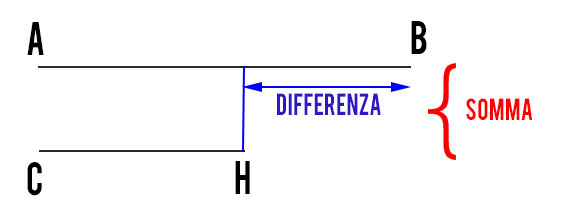
Quello che si nota è che se facendo la sottraendo la somma alla differenza e dividendo per due, si ottiene proprio il segmento più corto. Per cui:
Media=CH=(SOMMA-DIFFERENZA):2=(44-12):2=32:2
CH=16 cm
A questo punto possiamo calcolare il primo lato facendo la formula inversa di una delle due dateci dalla traccia:
AB+CH=44 → AB=44-CH=44-16
AB=28 cm
Possiamo ora finalmente calcolare l’area del triangolo scaleno.
A=b×h:2=28×16:2=224 cm²
La lezione che hai letto ti è stata utile? Hai dei dubbi o delle curiosità? Lascia un commento qui sotto… Il parere dei nostri studente è sempre importante per migliorare la qualità di un servizio che è GRATUITO e sempre lo resterà.
Approfondimenti: Triangolo rettangolo isoscele – Come si calcolano perimetro ed area?
In un triangolo scaleno ottusangolo,sappiamo ke il lato AB misura 99.0. Il latoAC misura 91.2. Quale la formula per trovare la misura del lato corto BC?
Ciao Roberto,
per capire come aiutarti avrei bisogno di sapere il tuo livello scolastico. E’ un esercizio per quale classe? Se è un triennio scuole superiori si può risolvere con la trigonometria, altrimenti bisogna assegnare un’incognita x.
Segnalo una svista: con riferimento alla formula di Erone qui indicata al punto 2 in quel caso p è proprio il perimetro, non il semiperimetro! perché nella formula p compare con al denominatore 2, ossia p/2.
Grazie per la segnalazione. Abbiamo già provveduto a correggere il refuso. 😉