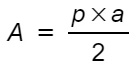L’ennagono è un poligono avente 9 lati e quindi 9 angoli. Si definisce invece ennagono regolare il poligono caratterizzato dalla presenza di 9 lati e 9 angoli tutti uguali.
In questa lezione vedremo qual è l’ennagono, quali sono le sue proprietà e le formule da usare negli esercizi. Dedicheremo anche una sezione alla costruzione di questo poligono regolare con squadretta e compasso.
Che cos’è l’ennagono?
Etimologia e significato della parola
La parola deriva dal greco e può essere suddivisa in due:
- enna = da ennèa significa 9
- gono = da gonia significa angolo
Definizione di ennagono
In base al significato della parola possiamo scrivere che l’ennagono è un poligono composto da 9 angoli. In alternativa possiamo anche dire che è una figura geometrica piana composta da 9 lati.
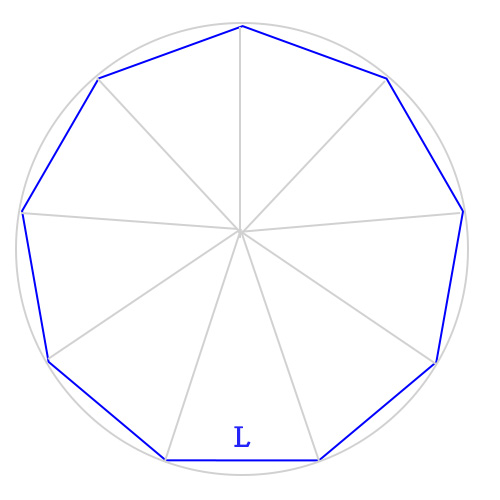
Quando tutti i lati sono uguali, allora si ha un ennagono regolare, come la figura che segue.
Proprietà dell’ennagono
Possiamo calcolare l’angolo che si forma ad ogni vertice della figura con la formula:
somma degli angoli interni = S = (n-2)·180 = 7·180 = 1.260
L’angolo dell’ennagono regolare sarà:
α = S : 9 = 1.290 : 9 ≅ 140°
Proprietà 1
L’angolo al vertice dell’ennagono misura circa 140° (in realtà misura 143,3 periodico)
Proprietà 2
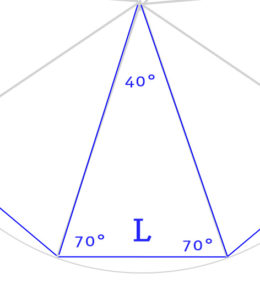
Suddividendo la figura in spicchi come abbiamo fatto nella figura in alto, otteniamo 9 triangoli isosceli. Poiché il loro angolo al vertice è 360°:9=40°, gli angoli alla base misura (180°-40°):2=70°.
Ennagono regolare formule
Come tutti i poligoni regolari, esistono due costanti che permettono di calcolare area e apotema noto il lato.
Numero fisso
Lato e apotema di un poligono regolari sono direttamente proporzionali secondo un coefficiente f, detto numero fisso. Risulta cioè:
a = f · L
E’ un numero che varia a seconda della figura considerata. Il numero fisso dell’ennagono regolare è:
f = 1,374
Costante d’area
L’area di un poligono regolare è proporzionale al quadrato del suo lato secondo un coefficiente φ, detto costante d’area.
φ = 6,182
Perimetro dell’ennagono
Noto il lato, essendo un poligono regolare, è sufficiente moltiplicarlo per 9 per ottenere la misura del perimetro.
p = 9 · L
Area dell’ennagono
In questo caso ci sono 2 formule in base ai dati disponibili.
- Se è noto il lato:
A =φ · L²
L’area è pari alla costante d’area moltiplicato per il lato al quadrato.
- Se è noto l’apotema:

Ovviamente sfruttando le formule inverse è possibile calcolare il lato ed apotema.
Costruzione dell’ennagono regolare
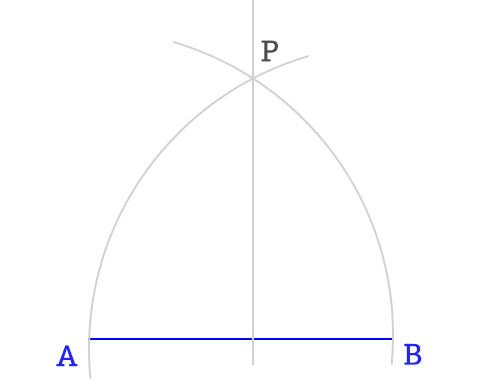
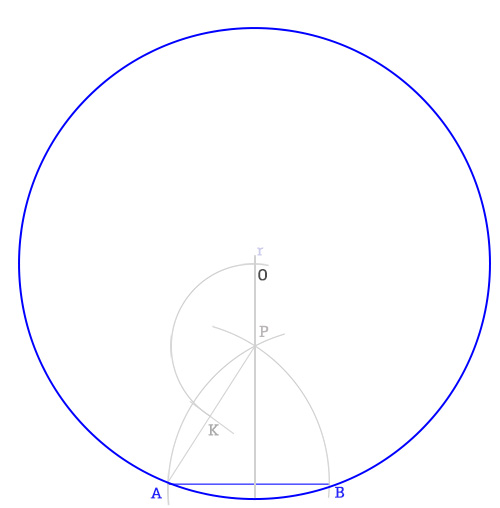
- Iniziamo disegnando il lato AB con una squadretta e di questo segmento ne disegniamo l’asse che chiamiamo r.

- A questo punto con il compasso, raggio AB, puntiamo in A e tracciamo una circonferenza. Poi in B e facciamo lo stesso. In questo modo si trova il punto P.

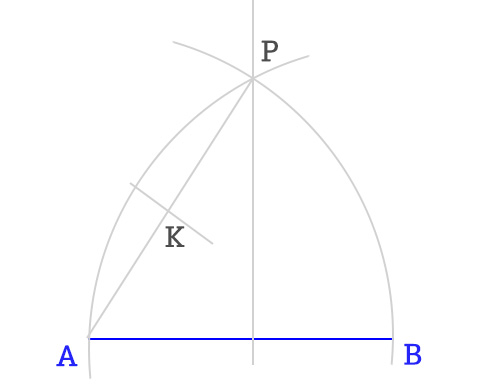
- Tracciamo l’asse s del segmento AP trovando così il punto K.

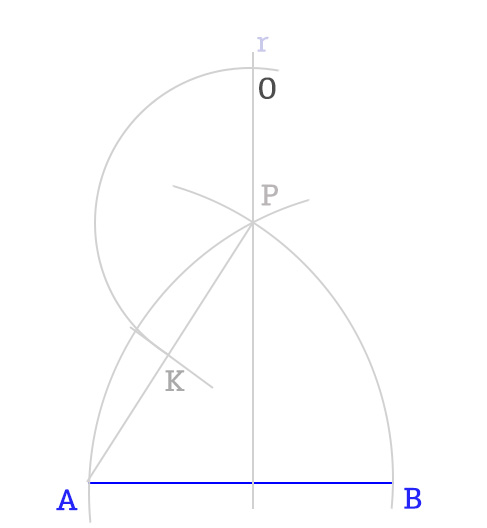
- A questo punto con il compasso, centro in P, raggio PK, traccio un arco e trovo il punto O sul primo asse disegnato.

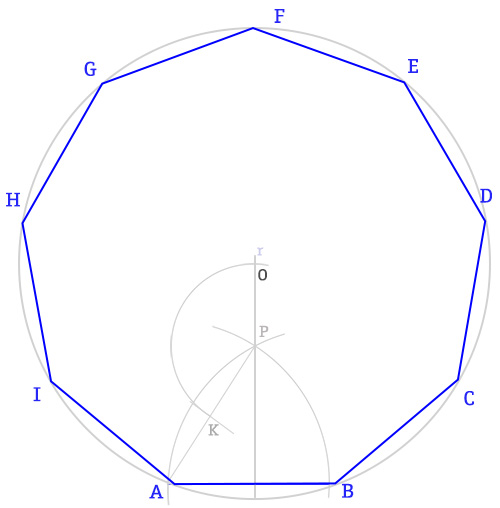
- Ricordi la costruzione del dodecagono? Si procede allo stesso modo. Quindi centro in O, apertura OB e si disegna la circonferenza circoscritta all’ennagono.

- A questo punto, compasso puntato in B, apertura AB e si trova C. Mantenendo la stessa apertura, si punta in C per ottenere D e si prosegue così fino a tornare al punto A.

Esercizio
Dato l’ennagono regolare di lato AB=10 cm, calcolare il perimetro e l’area.
Svolgimento
Per calcolare il perimetro semplicemente moltiplico il alto per 9.
P = 9 L = 9 · 10 = 90 cm
Sfrutto la costante d’area per il calcolo della superficie dell’ennagono.
A =φ · L² = 6,182 · 10² = 618,2 cm².