Si chiama Teorema di Carnot oppure Teorema del Coseno e permette di calcolare rapidamente la misura di un lato di un generico triangolo date le misure degli altri due lati e del loro angolo compreso.
Questo teorema si traduce in una formula trigonometrica estremamente utile nello svolgimento di esercizi e problemi. Assieme al teorema dei seni, il teorema del coseno (o teorema di Carnot) è una delle poche formule applicabili a qualsiasi tipo di triangolo.
Definizione teorema di Carnot (o teorema del coseno)
Enunciato: in ogni triangolo, il lato di un quadrato è pari alla somma dei quadrati degli altri due lati meno il doppio prodotto dei due lati per il coseno dell’angolo tra loro compreso.
Sembra difficile da ricordare eppure, tra poco, ti renderai conto di quanto questo teorema sia semplice. Cerchiamo di tradurre con linguaggio matematico la definizione del teorema del coseno.
Formula di Carnot
Disegniamo innanzitutto un generico triangolo assegnando nomi a vertici ed angoli.
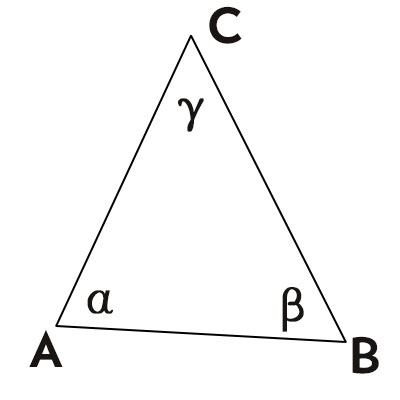
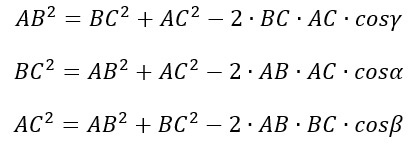
Spiegazione semplificata
Vediamo passo passo come l’enunciato ci porta alla formula. Dato il generico triangolo ABC, vogliamo calcolare il lato AB.
Il teorema del coseno ci dice che il lato AB al quadrato è pari alla somma dei quadrati degli altri due lati…
![]()
… meno il doppio prodotto di questi due lati per il coseno dell’angolo tra loro compreso. Gli altri due lati sono BC e AC, mentre l’angolo compreso tra questi lo abbiamo indicato con la lettera γ. Per cui la formula sarà:
![]()
Ovviamente il calcolo si può ripetere con tutti i lati del triangolo, ecco la ragione per cui abbiamo scritto 3 formule per il teorema di Carnot.
Dimostrazione del teorema del coseno
Vediamo a questo punto come si dimostra il teorema di Carnot. Disegniamo il triangolo generico e l’altezza relativa al lato AB.
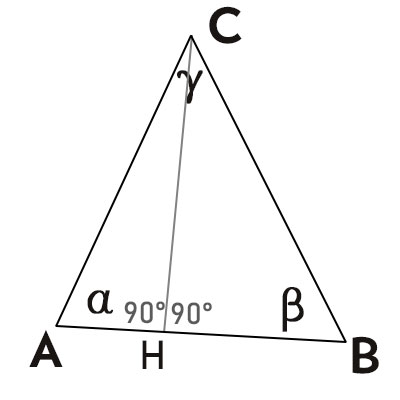
Consideriamo il triangolo rettangolo AHC ed utilizziamo le formule dei teoremi sui triangoli rettangoli in trigonometria. Possiamo così calcolare quindi l’altezza disegnata CH e il cateto AH e il in funzione del lato noto AC, ipotenusa del triangolo AHC.
Cateto = ipotenusa per il seno dell’angolo opposto o per il coseno dell’angolo adiacente
CH = AC · senα
AH = AC · cosα
Osservando il triangolo ABC, in particolar modo il segmento AB, possiamo notare che vale la relazione:
AB = AH + HB e quindi HB = AB-AH (abbiamo solo spostato i membri dell’equazione da una parte all’altra cambiando i segni).
Avendo calcolato AH, possiamo sostituire:
HB = AB – AH → HB = AB – AC cosα
Applichiamo a questo punto il teorema di Pitagora al secondo triangolo rettangolo BCH.
![]()
Sostituiamo con HB appena calcolato e con l’HC che abbiamo calcolato prima (evidenziato in grassetto).
![]()
Sviluppiamo le operazioni algebriche. Da notare che al secondo membro c’è un quadrato di binomio, per cui non dimentichiamoci del doppio prodotto.
![]()
Osserviamo che c’è un termina con AC² che può essere messo in evidenza. Facciamo quindi il raccoglimento a fattor comune.
![]()
Una delle relazioni fondamentali della trigonometria sottolinea come il seno al quadrato più il coseno al quadrato sono pari a 1, per cui:
![]()
(Dimostrazione terminata – come volevasi dimostrare)
Teorema del coseno e teorema di Pitagora
Osservando bene la formula, ti renderai conto che il teorema di Carnot è molto simile al teorema di Pitagora, con la differenza che il primo è valido per tutti i triangoli, il secondo solo per i triangoli rettangoli.
Infatti si dice che il teorema del coseno è una generalizzazione di Pitagora. Avendo il triangolo rettangolo un angolo pari a 90° ed essendo il coseno di 90° pari a 0, allora applicando Carnot ottieni proprio la formula del teorema di Pitagora
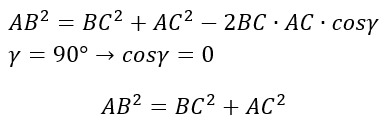
Esercizi con il teorema del coseno
Problema 1
Dato il triangolo ABC, calcolare la misura del lato AB sapendo che gli altri due lati misurano 5 e 10 cm e l’angolo tra essi compreso ha ampiezza pari a 30°.
Svolgimento
Abbiamo già tutti i dati a disposizione per applicare il teorema di Carnot. Scriviamo quindi subito la formula:
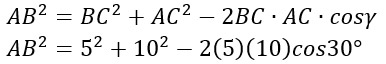
Poiché il coseno di 30 gradi è pari a radical 3 fratto 2, allora il risultato sarà:
AB = 6,2 cm
Problema 2
Determinare la misura di uno degli angoli del triangolo che ha per lati a=√3cm b=1cm e c=2cm
Svolgimento
In questo caso, visto che ci viene chiesto di calcolare l’ampiezza degli angoli, dovremo far riferimento alle formule inverse del teorema del coseno.
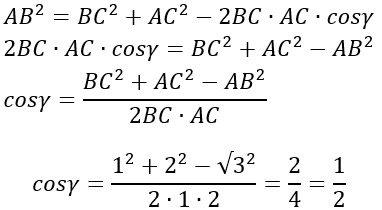
A questo punto possiamo calcolare l’angolo dal coseno semplicemente sfruttando l’arcocoseno.
γ = arccos(1/2) = 60°
Conclusioni
In questa lezione abbiamo studiato in maniera approfondita il teorema di Carnot. Abbiamo visto quando e come applicarlo agli esercizi e problemi.
Se dovessero esserci ancora dubbi sull’argomento, non esitare a lasciare un commento. Se questa lezione ti è stata utile, lascia un commento positivo, ci aiuterà a crescerà e a migliorare giorno per giorno la qualità degli appunti.