Le equazioni letterali di primo grado sono delle equazioni in cui, oltre ai coefficienti e all’incognita x, compaiono anche delle lettere. Generalmente nelle equazioni letterali si usano le lettere x, y, t, u, z come incognite mentre vengono utilizzate le lettere a, b, c, d, … come parte letterale.
Nella lezione di oggi vedremo come si risolvono le equazioni letterali intere e fratte. Vedremo come comportarci con le lettere, visto che in genere mettono in difficoltà tutti gli studenti. Nell’ultima parte della lezione, svolgeremo assieme una piccola esercitazione studiando degli esempi già svolti e commentati.
Per risolvere le equazioni letterali è fondamentale conoscere quelle che sono le tecniche di risoluzione delle equazioni di primo grado. Iniziamo subito.
Come risolvere equazioni letterali
Le equazioni con le lettere, come già anticipato, sono delle espressioni algebriche in cui compare l’incognita x e altre lettere. Queste si comportano come se fossero dei numeri, quindi dei coefficienti.
Come si calcolano le lettere? Non si calcolano. Dovrai portartele avanti e mantenerle fino alla soluzione. Vediamo un esempio pratico:
F=m·a
Quella che ti abbiamo appena scritto è una formula che si studia in fisica. E’ la seconda legge di Newton che sottolinea come la forza è pari alla massa per l’accelerazione. Matematicamente questa si traduce in un’equazione letterale in cui la massa m è una costante, cioè un numero.
Come si risolvono le equazioni letterali? Esattamente come le equazioni di primo grado. Inizia ad isolare l’incognita x al primo membro, mentre tutto il resto va a destra dell’uguale. Dividi tutto per l’eventuale coefficiente della x e hai trovato la soluzione.
Un esempio concreto di equazioni letterali intere lo abbiamo già visto quando abbiamo parlato delle equazioni di primo grado generiche. Dicemmo infatti che l’equazione:
ax+b=0
si risolve portando la lettera b al secondo membro e poi dividendo tutto per a. Scrivendo tutti i passaggi ho quindi:
ax=-b
(a/a)x=-(b/a)
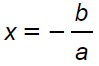
Equazioni letterali fratte
Merita un approfondimento il caso in cui la x compare al secondo membro. In questo caso il procedimento diventa leggermente più complesso. Ti ricordi come si risolvono le equazioni fratte di primo grado? Bisogna calcolare il minimo comune multiplo ed imporre delle condizioni di esistenza. Le lettere dell’equazione non influenzano in alcun modo lo svolgimento.
Esempio
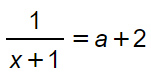
Per prima cosa è necessario scrivere sulla destra le condizioni di esistenza. Per cui imponiamo il denominatore diverso da 0.
C.E.
x+1≠0 → x≠-1
A questo punto possiamo calcolare il minimo comune multiplo.
mcm=x+1
Riscriviamo l’equazione dividendo il mcm per il denominatore di ogni frazione. Da notare che al secondo membro, il denominatore è sottinteso e vale 1. A quel punto possiamo poi eliminare il denominatore.
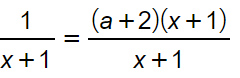
(a+2)(x+1)=1
A questo punto si tratta di risolvere una moltiplicazione di polinomi al primo membro. Per cui otteniamo:
ax+a+2x+2=1
Nelle equazioni letterali, come detto, lasciamo i termini con la x a sinistra e tutto il resto va a destra, eseguendo dove necessario le somme algebriche tra termini o monomi simili.
ax+2x=1-2-a
x(a+2)=-(1+a)
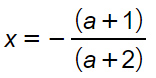
Equazioni letterali esercizi
Come hai potuto vedere, le equazioni con le lettere non sono un argomento particolarmente complesso. Con le equazioni letterali di secondo grado sarà già un po’ diverso, ma per poter trattare quell’argomento bisogna prima studiare le equazioni di secondo grado.
Inizia ora questa seconda parte della lezione in cui vedremo alcuni esercizi svolti sulle equazioni letterali.
Esercizio 1
10=2πx
Svolgimento
Abbiamo deciso di risolvere questo esercizio perché è importante che ti abitui ad avere delle equazioni letterali con il pi greco, perché quando studierai trigonometria sarà una costante molto presente. Il π però non cambia il metodo risolutivo dell’equazione.
x=10/(2π)
x=5/π
Esercizio 2
π(x+3)-2π=(1/2)x+4π
Svolgimento
Leggermente più complessa della precedente iniziamo a risolvere la moltiplicazione al primo membro e poi ordiniamo l’equazione letterale di primo grado tenendo la x a sinistra.
πx+3π-2π=(1/2)x+4π
πx-(1/2)x=4π-3π+2π
Sommiamo algebricamente i termini simili che abbiamo segnato in azzurro.
πx-(1/2)x=4π-3π+2π
πx-(1/2)x=3π
A questo punto eseguiamo una messa in evidenza totale al primo membro raccogliendo la x.
x(π-1/2)=3π
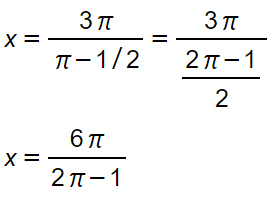
Esercizio 3
2πx−3(π−1)=πx−2π
Svolgimento
2πx−3π+3=πx−2π
2πx-πx=-2π+3π-3
πx=π-3
x=(π-3)/π
Problema
Data l’equazione della retta y=mx+q, calcolare il valore di m.
Svolgimento
L’equazione della retta la studierai nel programma di geometria analitica. Come ogni formula scritta in termini generali, si presenta come un’equazione letterale. Il nostro obiettivo è risolverla considerando m come incognita. Per cui bisogna isolare la m al primo membro.
y=mx+q
mx=y-q
m=y/x – q/x
In questo caso, le lettere dell’equazione sono x,y e q. Mentre l’incognita calcolata è la m.