Come si risolve una somma algebrica? Che differenza c’è tra le somme algebriche e le normali addizioni tra numeri interi? Avrei bisogno di una spiegazione chiara con qualche esempio che riguardi anche le frazioni. Grazie, Luca.
Risposta
La somme algebriche sono delle addizioni o delle sottrazioni tra numeri relativi. Questo significa che una somma algebrica può essere sia una somma che una differenza. Cerchiamo di essere più chiari sin da subito e di vedere un esempio concreto.
![]()
Quella che hai appena visto è una somma algebrica tra numeri relativi. Essendo una somma, non cambia l’ordine degli addendi, per cui possiamo scrivere che -10+12 è equivalente a +12-10.
Approfondimenti: vedi tutte le operazioni con i numeri relativi
Questa, che fino a qualche anno fa avresti considerato una banale sottrazione, può essere vista come la somma algebrica di un numero (+12) e l’opposto del secondo (-10). Cioè possiamo scrivere:
+12-10 = +12+(-10)
E’ proprio per questa ragione che, una volta che a scuola si è introdotto il concetto di numero relativo, non si parla più di addizione e sottrazione, ma semplicemente di somma algebrica.
Come si fa la somma algebrica?
Possiamo distinguere due semplici casi: quello in cui i numeri sono concordi e quello in cui sono discordi.
Somme algebriche tra numeri concordi
Siano dati due numeri relativi con lo stesso segno, quindi concordi. La somma algebrica si calcola facendo semplicemente sommando le due parti numeriche e conservando il segno.
Esempio 1:
-3-5
Poiché i numeri hanno entrambi il meno, mantengo il segno e faccio l’addizione dei numeri.
-3-5=-8
Esempio 2:
+3+5
Poiché i numeri hanno entrambi il segno più, si mantiene il segno e si addizionano le parti numeriche.
+3+5=+8
Somma algebrica tra numeri discordi
Se i due numeri hanno segno opposto, allora si mantiene il segno della parte numerica maggiore e si esegue la sottrazione dei due numeri. Ovviamente ricordati di sottrarre il maggiore meno il minore.
Esempio 1
+3-5
Le due parti numeriche sono 5 e 3, dove ovviamente cinque è maggiore di 3. Per cui conservo il segno del 5 ed eseguo la sottrazione 5-3=2 a cui devo aggiungere il segno.
+3-5=-2
Esempio 2
+27-15
Poiché 27 è maggiore di 15, si conserva il segno + e si fa la sottrazione 27-15=12
+27-15=+12
Somma algebrica di frazioni
Quando ti trovi a dover eseguire la somma di numeri relativi sotto forma di frazione, diventa tutto estremamente meccanico.
- Calcola il minimo comune multiplo
- Dividi il mcm per il primo denominatore e moltiplicalo per il primo numeratore, conserva il segno.
- Esegui questa operazione per ogni numero da addizionare.
- Disponi i numeri sotto un unico denominatore.
- Addiziona gli elementi al numeratore della frazione.
Esempio 1
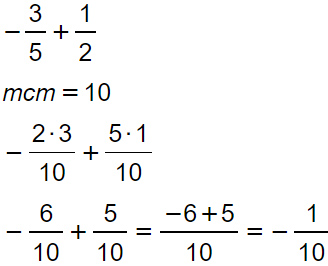
Come puoi vedere 5 e 2 concorrono a formare il minimo comune multiplo (10). Poi riscriviamo le due nuove frazioni con il mcm al denominatore e si sommano i numeratori. Si arriva presto al risultato.
Esempio 2
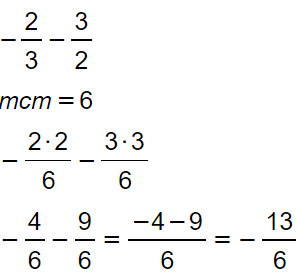
Conclusioni
L’argomento che abbiamo approfondito oggi sarà estremamente utile in tutto il programma di algebra. Infatti parleremo più avanti di somma algebrica di polinomi, di monomi e di radicali. Per ora ti basta sapere come si fa la somma algebrica tra due numeri relativi.
Se questa lezione ti è stata utile o hai ancora dubbi e incertezze, lascia un commento in basso. Ci sarà utile per migliorare la qualità delle lezioni. Il nostro staff ti risponderà nel minor tempo possibile.
Molto chiaro, grazie!