L’equazione della retta nel piano cartesiano rappresenta tutti i punti che appartengono alla generica retta r. In geometria analitica essa si descrive attraverso un’equazione di primo grado con le incognite x e y.
In questa lezione vedremo qual è l’equazione di una retta generica, quali sono le variabili da calcolare e le formule da utilizzare negli esercizi e nei problemi. Parleremo di forma implicita esplicita, di condizioni di appartenenza e vedremo alcuni casi particolari, come l’equazione della retta per due punti. Alla fine di questa guida troverai alcuni problemi svolti e commentati.
Primi di vedere qual è l’equazione generale della retta, facciamo un breve ripasso su questo ente geometrico fondamentale che si studia anche nelle scuole primarie. Che cos’è la retta? E’ un insieme infinito di infiniti punti allineati.
La formula della retta può essere scritta in due diversi modi, cioè in due forme che permettono di risolvere ogni tipo di esercizio o problema. Stiamo parlando della forma esplicita ed esplicita. Sono perfettamente equivalenti e spetterà poi a te decidere quale utilizzare. Ecco le due equazioni della retta.
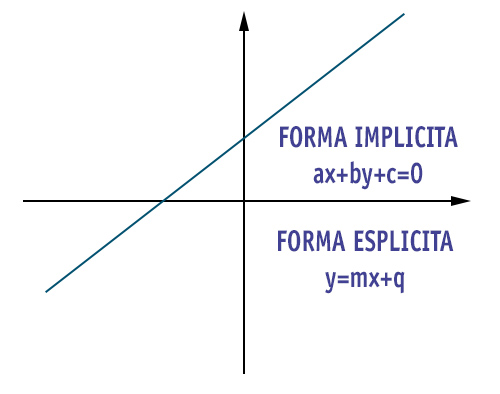
Equazione della retta in forma implicita
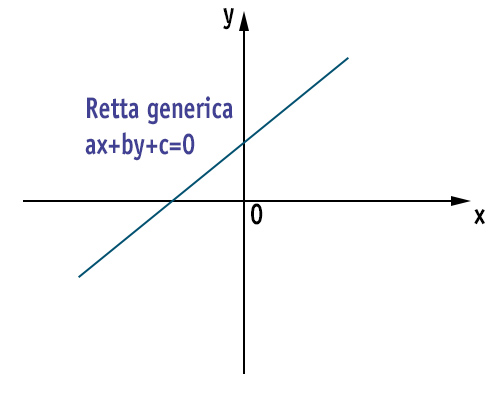
ax+by+c=0
Ti ricordiamo che le incognite sono x e y, mentre a,b e c sono dei coefficienti numerici che individuano in maniera precisa ed univoca la posizione nel piano cartesiano della retta. Possiamo a questo punto distinguere 3 casi:
- Se a=0, l’equazione della retta diventa
by+c=0 → y=-b/c
Anche by+c è un’equazione di primo grado, per cui rappresenta anch’essa la formula di una retta. Tuttavia manca l’incognita x. In questo caso abbiamo una retta che mantiene la sua y sempre costante, cioè pari a -b/c. Si tratta quindi dell’equazione di una retta orizzontale.
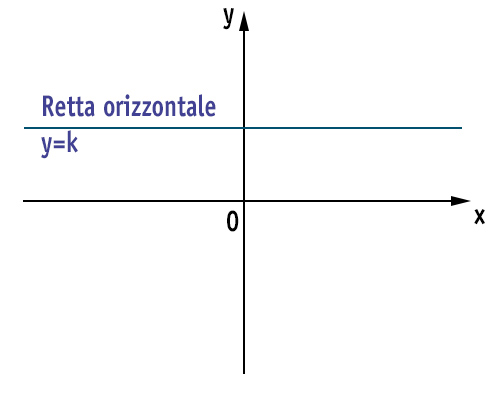
PROMEMORIA: quando quindi trovi una retta a cui manca la x e che si presenta nella forma y=k, dove k può essere un numero qualsiasi, anche una frazione o una radice, allora hai una retta orizzontale.
- Se b=0, l’equazione della retta implicita diventa:
ax+c=0 → x=-c/a
Ho quindi un’equazione di primo grado con un’unica incognita, la x che è costante e pari a -c/a. Se la x deve restare sempre uguale, vuol dire che ho una retta verticale.
Quando quindi ho una formula con x=numero vuol dire che sto parlando di una retta verticale.
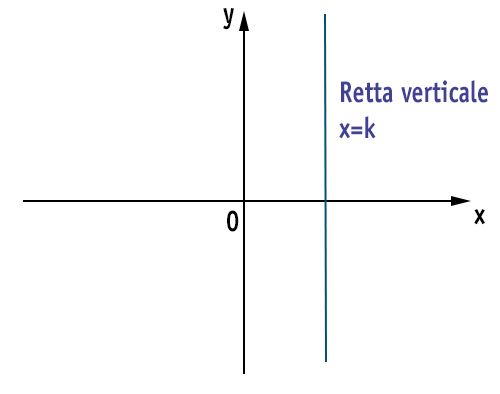
PROMEMORIA: quando trovi una retta a cui manca la y e si presenta nella forma x=k, dove k è un qualsiasi numero, allora hai una retta verticale, cioè parallela all’asse delle y.
- Se c=0, l’equazione della retta implicita diventa:
ax+by=0
Che rappresenta l’equazione della retta passante per l’origine degli assi (di qualsiasi inclinazione)
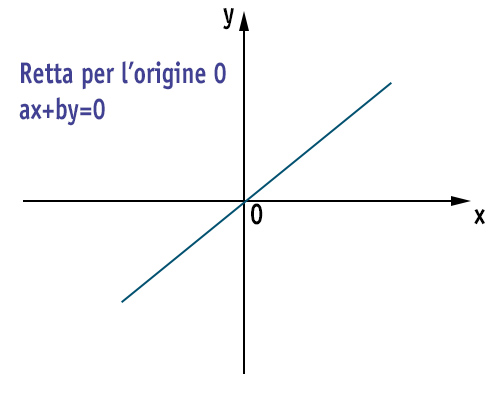
- Se tutti i coefficienti della retta sono diversi da zero, allora ho semplicemente l’equazione della retta generica espressa in forma implicita

Equazione della retta in forma esplicita
La forma più utilizzata per esprimere l’equazione della retta generica è attraverso l’uso della forma esplicita. E’ la più usata perché, vedremo, permette già subito di capire in maniera approssimativa come sarà il grafico. L’equazione della retta esplicita è:
y=mx+q
dove m è il coefficiente angolare della retta, q è l’intercetta sull’asse delle ordinate o termine noto.
Che cos’è il coefficiente angolare m?
Il coefficiente angolare di una retta indica semplicemente la sua inclinazione. Se il coefficiente angolare è positivo allora la retta tenderà all’infinito al primo e terzo quadrante. Se m<0, allora la retta sarà inclinata in modo che all’infinito si troverà nel secondo e quarto quadrante.
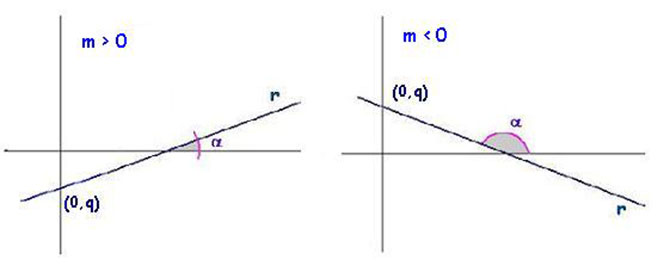
1- Coefficiente angolare Positivo 2- Coefficiente angolare negativo
Il termine noto, o intercetta sull’asse delle ordinate, invece, molto semplicemente mi dice a quale ordinata la retta si interseca con l’asse y. Nell’ultima immagine possiamo vedere che in entrambe le rette (sia per coefficiente angolare negativo che positivo) il termine noto è q, cioè l’ordinata del punto di intersezione tra retta e asse y.
Quando un punto appartiene ad una retta?
Si tratta di una verifica che si rende talvolta necessaria nello svolgimento degli esercizi. Verificare se il punto appartiene alla retta (o a una qualsiasi figura) è semplicissimo: è sufficiente andare a sostituire le coordinate del punto all’interno della formula della figura e verificare che il primo membro sia uguale al secondo membro.
Verificare che il punto 0(0;0) appartiene alla retta y=4x. Sostituisco x=0 e y=0 (cioè le coordinate dei punti) all’interno della formula della retta, per ottenere zero uguale a zero. Se i membri non fossero stati uguali, allora il punto non sarebbe appartenuto alla retta.
Equazione della retta passante per due punti
Per prima cosa verifichiamo che i due punti non abbiano stessa ascissa o stessa ordinata. Nel primo caso infatti avremmo una semplice retta verticale (di equazione y=l’ascissa in comune), nel secondo caso una retta orizzontale (di equazione x=ordinata in comune).
Imponiamo il passaggio dei due punti (A e B) per la retta generica di equazione y=mx+q. Sostituiamo la x e la y di A nell’equazione della retta generica y=mx+q. Faccio la stessa cosa con il punto B ed ottengo così due equazioni dove le incognite sono m e q. Risolvo con un sistema di equazioni di primo grado e ottengo il risultato. Vediamo con un esempio: troviamo l’equazione della retta passante per due punti A(0;0) B(1,2)
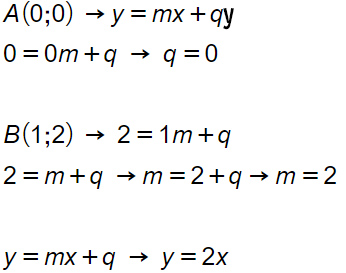
Come disegnare una retta data l’equazione
Il nostro consiglio è di trasformare l’equazione della retta sempre in forma implicita, cioè y=mx+q. Una volta arrivati a questo punto ci costruiamo un piccolo schemino in cui andiamo ad assegnare due valori a nostra scelta alla x, calcolando la y di conseguenza. Otterremo così due punti, basta disegnarli, congiungerli e otteniamo quindi la retta.
Vediamo con un esempio pratico, come muoverci. Disegnare la retta di equazione y=3x-2.
- Assegno un primo valore arbitrario alla x. Ad esempio x=0. Lo sostituisco nell’equazione della retta: y=3x-2=0-2=-2. Ho ottenuto il punto di coordinate (0;-2)
- Assegno un secondo valore arbitrario alla x. Ad esempio x=1. Lo sostituisco nell’equazione della retta data: y=3x-2=1. Ho ottenuto il secondo punto di coordinate (1;1)
- Disegno la retta sul piano cartesiano.
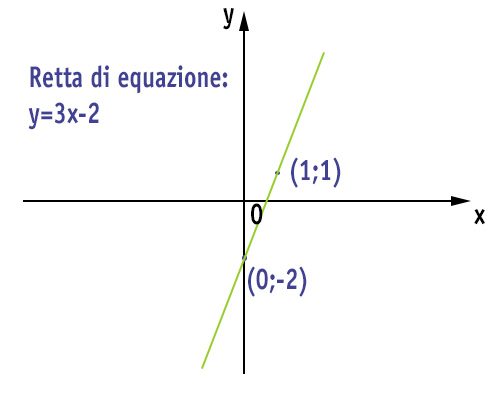
Il metodo è valido per l’equazione della retta in forma implicita ed esplicita.
Esercizi sull’equazione della retta
Esercizio 1
Scrivere l’equazione del luogo dei punti di ascissa -9
Svolgimento
Quando trovi una traccia con questo tipo di richiesta, vuol dire che dobbiamo trovare l’equazione di una retta in cui tutte le y siano pari a -9. Tradotto in linguaggio matematico, questo significa che y=-9. Questa è l’equazione di una retta orizzontale che si trova sotto l’asse delle ascisse. Dato che non ci viene richiesto il grafico, l’esercizio è concluso.
Esercizio 2
Determiniamo l’equazione delle retta passante per due punti A(2,3) B(0;4)
Svolgimento
Non avendo ancora studiato l’equazione della retta per due punti, usiamo il metodo visto sopra. Cioè sostituiamo prima il punto A nella formula della retta e poi il punto B. Iniziamo subito.
y=mx+q
A(2;3) → 2m+q=3
B(0;4) → 0x+q=4 → q=4
Sostituiamo il valore di q trovato nella prima equazione come se fosse un normale sistema di primo grado per ottenere così:
q=4
2m+4=3 → 2m=-1 → m=-1/2
Per cui l’equazione della retta è: y=-1/2 m + 4.
Esercizio 3
Scriviamo l’equazione della retta r passante per O(0,0) e A(+2,-3) e verifichiamo che il punto B(1,1) non vi appartiene e il punto C(-4,+6) vi appartiene.
Svolgimento
La prima parte dell’esercizio è identica alla precedente. Per cui risolviamo subito:
y=mx+q
0(0;0) → 0=0m+q → q=0
A(+2;-3) → 2m+q=3
Sostituisco il valore di q, per ottenere:
2m+0=3 → m=3/2
L’equazione della retta per i due punti è:
y=3/2 x
Dobbiamo verificare ora l’appartenenza del punto B(1;1) e C(-4;+6) alla retta. Sostituiamo le sue coordinate nella formula della retta appena trovata e vediamo se ci esce un’identità o meno.
y=3/2x
B(1;1) → 1=3/2(1) → Impossibile, il punto non appartiene alla retta.
C(-4;+6) → 6=3/2 (4) → 6=6 E’ un’identita, il punto appartiene alla retta.
Esercizio 4
Determiniamo il coefficiente angolare della retta s:-6x+2y+3=0
Svolgimento
Per calcolare il coefficiente angolare m di una retta, è necessario passare da forma implicita a esplicita. Per farlo basta isolare la y al primo membro dell’equazione.
-6x+2y+3=0
2y=6x-3
y=3x-3/2
Il coefficiente angolare è m=3.
Conclusioni
Termina così la lezione su equazioni e formule della retta. Troverai nelle prossime lezioni degli approfondimenti che consigliamo di leggere. Se intanto hai dei dubbi o se questi appunti ti sono stati utili, lascia un commento in basso. Ci aiuterai a migliorare la qualità delle lezioni, con la possibilità di offrirti sempre contenuti di qualità e gratis.
Approfondimenti:
Nell’esempio della retta passante per 2 punti avete messo il valore di x nella y del punto B (1;2)
Grazie Paola, siamo lieti che i nostri studenti ci segnalino gli errori.
Ovviamente abbiamo già provveduto a caricare la correzione. Grazie e continua a seguirci…