Equazioni fratte – come si risolvono le equazioni frazionarie di primo grado?

Si chiamano equazioni fratte di primo grado quelle equazioni in cui l’incognita compare anche al denominatore di una frazione algebrica. Attraverso pochi passaggi matematici vengono ricondotte alle equazioni di primo grado. Vengono chiamate anche equazioni frazionarie e hanno la caratteristica di essere lineari, cioè l’incognita x non è elevata a potenza.

Per poter risolvere equazioni di primo grado fratte è necessario conoscere i metodi risolutivi che abbiamo già visto nella lezione sulle equazioni di primo grado. All’interno della lezione di oggi ci soffermeremo sulle equazioni frazionarie, analizzandone metodi risolutivi e alcuni semplici esercizi e suggerimenti che ti permetteranno di evitare errori.

Il metodo che analizzeremo tra poco sarà valido per tutti i tipi di equazioni fratte, sia di primo che di secondo grado. Per cui è importante imparare ora la tecnica risolutiva per poi poterla ripetere anche negli argomenti futuri.

Quali sono le equazioni fratte?

Come detto sono quelle equazioni che presentano delle frazioni con l’incognita x presente almeno una volta al denominatore. La forma base a cui dovrai sempre cercare di ricondurti è la seguente.

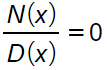
Quella che hai appena visto in figura viene chiamata forma normale di un’equazione fratta. Indica il rapporto tra un polinomio al numeratore N(x) e un polinomio al denominatore D(x).

CONSIGLIO → come puoi vedere al secondo membro c’è 0. Quando hai degli esercizi sulle equazioni frazionarie, ricordati di portare tutto al primo membro, così da evitare errori durante i vari passaggi.

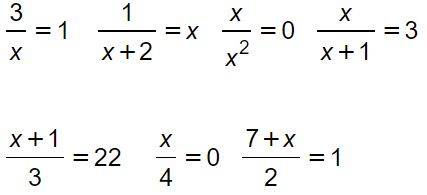
Mentre al primo rigo ti abbiamo indicato 4 equazioni fratte, le ultime 3 al secondo rigo non sono equazioni fratte. In queste ultime infatti l’incognita x non compare mai al denominatore.

Come risolvere le equazioni fratte di primo grado

1 – Le condizioni di esistenza

Il primo passaggio consiste nell’imporre le condizioni di esistenza. Che cosa sono? Sono delle condizioni che vanno a specificare quando l’equazione fratta può esistere nell’insieme dei numeri reali. Questo vuol dire che ci sono alcune soluzioni che non sono considerate accettabili. Come determinarle? Bisogna imporre un’unica condizione: denominatore diverso da zero.

D(x)≠0

PROVA A FARE UN ESPERIMENTO → Prova sulla tua calcolatrice a dividere un qualsiasi numero per 0. Qual è il risultato che ottieni? Una normale calcolatrice scientifica ti dà come risultato ERRORE. Questo perché non è possibile dividere un numero per 0.

Allo stesso modo, nelle equazioni fratte bisogna specificare esplicitamente che ogni singolo denominatore deve essere diverso da zero. In genere lo si mette sulla destra, in modo da poter sviluppare tranquillamente l’esercizio sulla sinistra. Se nell’esercizio ci sono 3 frazioni con la x, scriverò 3 condizioni di esistenza. Se ce ne sono 2, ne scriverò 2, eccetera…

2 – Riduzione alla forma normale

Solo dopo aver specificato e risolto le condizioni di esistenza possiamo risolvere le equazioni fratte. Come? Facendo il minimo comune multiplo (mcm) tra i polinomi presenti al denominatore.

Per ogni frazione eseguo la seguente operazione: mcm diviso denominatore per numeratore. Non dimenticarti di riportare i segni e cerca di fare tutti i calcoli utilizzando le parentesi tonde. L’obiettivo e quello di arrivare alla forma N(x)/D(x)=0, cioè alle forma normale.

3 – Eliminazione del denominatore

A questo punto possiamo eliminare il denominatore e imporre il nuovo polinomio al numeratore uguale a zero. A questo punto ti sarai ricondotto ad una normale equazione di primo grado e potrai arrivare alla soluzione generalmente in pochi passaggi.

4 – Verifica dei risultati

Al termine dell’esercizio sulle equazioni fratte avrai delle soluzioni del tipo x=n, cioè la x uguale a un numero. Dovrai verificare che ogni singolo risultato ottenuto non violi le condizioni di esistenza che hai esplicitato in precedenza. Accanto ad eventuali risultati non compatibili con le condizioni di esistenza, dovrai semplicemente scrivere: SOLUZIONE NON ACCETTABILE PER LE CONDIZIONI DI ESISTENZA.

Esempi di equazioni fratte

La spiegazione teorica è conclusa. A questo punto non resta che mettere in pratica quello che abbiamo imparato fino ad ora e provare a risolvere degli esercizi.

Esercizio 1

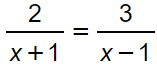
Si tratta sicuramente di un’equazione fratta, perché l’incognita x è presente in entrambi i denominatori. Dovremo quindi scrivere due condizioni di esistenza (C.E.).

C.E.

x+1≠0 → x≠-1
x-1≠0 → x≠+1

Una volta espresse le condizioni di esistenza, possiamo calcolare il minimo comune multiplo.

mcm=(x+1)(x-1)

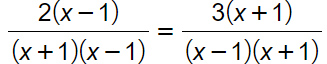
Che calcoli abbiamo fatto per arrivare a questo punto?

• Nella prima frazione abbiamo calcolato (x+1)(x-1):(x+1)·2
• Nella seconda frazione abbiamo calcolato (x+1)(x-1):(x-1)·2

Visto che nella forma normale al secondo membro c’è zero, portiamo tutto al primo membro e portiamo tutto sotto la stessa linea di frazione. Possiamo farlo ora che i denominatori sono identici.

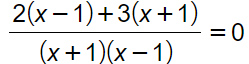
A questo punto il denominatore D(x) può essere eliminato e possiamo concentrarci solo sul numeratore, eseguendo le moltiplicazioni richieste dall’esercizio.

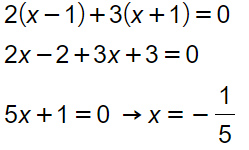
Come puoi vedere in pochi passaggi siamo arrivati alla soluzione che è perfettamente compatibile con le condizioni di esistenza. Per cui esercizi terminato.

Esercizio 2

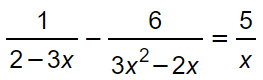
Quello che notiamo subito è che il secondo denominatore ha un termine al quadrato. Vediamo se possiamo subito ridurlo attraverso una delle tecniche di scomposizione di polinomi. In questo caso noto una x in comune per cui applico il raccoglimento a fattor comune totale.

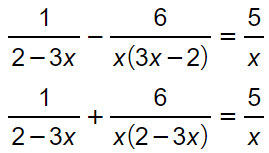
Nel secondo passaggio qui sopra abbiamo invertito il segno dell seconda frazione così da rendere il denominatore uguale al primo. A questo punto possiamo scrivere le condizioni di esistenza.

C.E.

2-3x≠0 → x≠+2/3
x≠0

Come fatto con l’esercizio precedente, scriviamo tutto sotto forma di un unico denominatore.

mcm=x(2-3x)

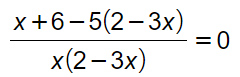
Eliminiamo il denominatore e concentriamoci esclusivamente sul numeratore:

x+6-10+15x=0

16x-4=0

x=4/16 → x=1/4

Conclusioni

Puoi continuare ad esercitarti con gli esercizi sulle disequazioni fratte. Troverai tanti esempi ed equazioni frazionarie svolte o da risolvere con cui fare pratica.

Se invece sulla parte teorica hai ancora dei dubbi o hai bisogno di chiarimenti, o anche se questa lezione ti è stata utile, lascia un commento in basso. Ci aiuterai a migliorare la qualità delle lezioni che ogni giorno ti mettiamo a disposizione gratuitamente.