Nella lezione di oggi impareremo a risolvere le equazioni di secondo grado, pure, spurie e complete. Analizzeremo i vari casi con esempi ed esercizi svolti e con la presenza di radicali, i nemici di tutti gli studenti.
Spiegazione sulle equazioni di secondo grado
- Come sono fatte le equazioni di II grado
- Equazioni pure e spurie
- Equazioni di secondo grado complete
- Formula ridotta
- Esercizi svolti e da svolgere
Ciò che non abbiamo mai incontrato negli esercizi sui sistemi di equazioni di primo grado è il simbolo della potenza. Tutti gli esercizi di matematica fino ad ora risolti, infatti, erano lineari, cioè nessuna di queste era elevata al quadrato. Oggi invece, studiando le equazioni di secondo grado, vedremo come comportarci di fronte ad un’espressione con il quadrato.
La forma canonica delle equazioni di II grado
La forma base, detta anche normale o forma canonica, di un’equazione di secondo grado è:
ax2+bx+c=0
Quante sono le soluzioni di un’equazione di secondo grado?
Nelle scorse lezioni abbiamo già evidenziato che il numero di soluzioni è sempre pari al grado del polinomio. Questo significa che un’equazione di primo grado avrà una sola soluzione, mentre le equazioni di secondo grado hanno due soluzioni, sempre. Per ogni caso che andremo ad analizzare le soluzioni saranno sempre e soltanto due.
Può capitare che siano uguali tra di loro, ma sono sempre due. Lo vediamo bene quando andiamo a risolvere le equazioni di secondo grado pure e in cui b=c=0
Equazioni di secondo grado pure e spurie
Si parla di equazioni pure e spurie quando uno o più coefficienti del trinomio sono uguali a zero. Ovviamente il primo coefficiente, la a, è sempre diversa da zero, altrimenti non avremmo un’equazione di secondo grado, ma di primo.
Può capitare invece che gli altri due coefficienti possano non esserci, cioè essere pari a 0. Possiamo così analizzare tre diversi casi.
-
b=c=0
In questo caso la forma canonica diventa, annullando b e c,
ax2=0 → x=0
Molto semplicemente questa equazione di secondo grado ammette come soluzione soltanto x=0. Ecco i passaggi per trovare la soluzione:
ax2=0 → x2=0 → x=0
Abbiamo cioè spostato il coefficiente a al secondo membro così come abbiamo imparato a fare negli esercizi sulle equazioni di primo grado. Per eliminare il quadrato è stato sufficiente fare la radice quadrata di entrambi i membri dell’equazione.
Da notare che, nonostante la soluzione ci sembri unica, cioè x=0, in realtà le soluzioni sono due: +0 e -0. Per semplicità si indica direttamente x=0.
Questo per due motivi. Il primo di carattere teorico – le equazioni di II grado hanno sempre due soluzioni – il secondo invece più pratico: quando risolvo la radice di un numero ne ottengo due.
Esempio:
√4=±2
La radice di 4 non fa 2, perché siamo nei numeri relativi, ma fa +2 e -2. Questo perché se facessimo l’operazione inversa, cioè il quadrato, sia -2 che +2 porterebbero alla stessa soluzione. Cioè 4. Quindi la radice quadrata di 4 fa +2 e -2.
-
Equazione di secondo grado pura (b=0)
Si parla di equazione di secondo grado pura quando il coefficiente del termine di primo grado è pari a zero. L’equazione diventa così:
ax2+b=0
Ti ricordi come risolvere le equazioni di primo grado? Se la risposta è no, ovviamente ti consigliamo di rileggere la lezione sulle equazioni di I grado. Qui non cambia assolutamente nulla, si portano i termini noti al secondo membro e si lasciano le incognite a sinistra.
ax2=-b
A questo punto si porta il coefficiente dell’incognita a secondo membro e, per eliminare la potenza, si fa la radice quadrata al primo e secondo membro.
x2=-b/a
x=±√(-b/a)
Come nel caso precedente avendo risolto una radice quadrata ho due soluzioni, una positiva e una negativa.
Esempio:
-2x2+1=0 → -2x2=-1 → 2x2=1 → x2=1/2 → x=±√1/2
-
Equazione di secondo grado spuria
Ci troviamo di fronte ad un’equazione di secondo grado spuria quando il termine noto è uguale a 0. Quando c=0, mi trovo in una situazione particolarmente vantaggiosa perché posso risolvere più rapidamente attraverso le regole per la scomposizione dei polinomi. Infatti, semplicemente con una messa in evidenza totale, posso risolvere l’esercizio:
x2-2x=0 → x(x-2)=0
A questo punto ricordandomi che se ho una moltiplicazione tra fattori uguali a zero (legge dell’annullamento del prodotto) posso risolvere imponendo ognuno pari a 0, posso risolvere l’esercizio trovando le due soluzioni:
x1=0 e x2=2
Approfondimento: guarda la lezione sulle equazioni spurie
Come risolvere un’equazione di secondo grado completa
Nel momento in cui nessuno dei coefficienti dell’equazione si annulla, ci troviamo di fronte ad un’equazione di II grado completa:
ax2+bx+c=0
La formula per risolvere le equazioni di secondo grado è:
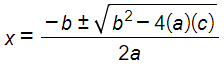
In questa formula risolutiva, applicabile sempre e comunque siamo in presenza di equazioni di secondo grado, ha un termine sotto radice chiamato discriminante e si indica con la lettera maiuscola greca Delta:
Δ=b2-4ac
Studiando le proprietà dei radicali, abbiamo visto che una radice non può essere mai negativa. Questo significa che il delta, il discriminante, non può mai essere minore di 0, ma solo maggiore o uguale di 0, altrimenti l’equazione si dice che non ammette soluzioni reali.
Esercizio svolto
3x2+2x-16=0
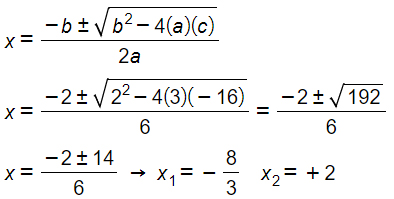
Come puoi vedere, in questo esercizio sulle equazioni di secondo grado, alla fine sono arrivato a calcolare la soluzione con pochi passaggi algebrici.
La formula ridotta per le equazioni di secondo grado
Quando il coefficiente b è pari, è possibile risolvere le equazioni di secondo grado sfruttando la formula ridotta con il delta quarti.
I docenti si preoccupano spesso a scuola che i ragazzi sappiano utilizzare bene questa formula, che in realtà, a nostro avviso a un’utilità piuttosto marginale. Il nostro consiglio è di memorizzare bene la formula generale, sapendo che esiste comunque anche la ridotta. Portano allo stesso risultato ma l’ultima può essere usata solo quando b è pari. Ecco un esercizio risolto:
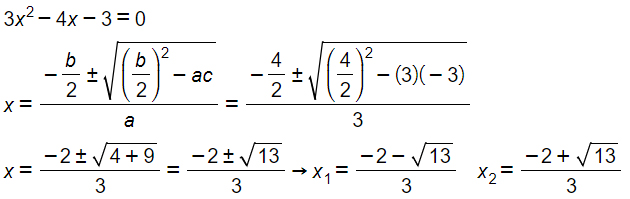
Da notare che le soluzioni finali sono delle radici. Come comportarci in questo caso? Nessun problema, la soluzione resta così com’è…
Vedremo nella prossima lezione degli esercizi svolti sulle equazioni di secondo grado. Ti consigliamo vivamente di esercitarti, perché quello che hai studiato oggi non è una nozione matematica difficile, ma che troverai molto di frequente nei prossimi anni.
Se ti restano dubbi sulla parte teorica, vuoi porci delle domande o vuoi chiederci informazioni, contattaci e verremo incontro ad ogni tua esigenza.