Le equazioni di secondo grado fratte sono delle equazioni di secondo grado frazionarie in cui al denominatore compare anche l’incognita x. Vengono dette anche equazioni frazionarie di grado 2 o equazioni razionali fratte e per poterle risolvere è necessario ricondurle a delle equazioni di secondo grado.
Proprio per questa ragione è importante conoscere la formula risolutiva delle equazioni di secondo grado, quindi sapere che cos’è e come si calcola il delta. Essendoci anche delle frazioni, dovremo calcolare anche il minimo comune multiplo. Vedremo comunque tutto con calma all’interno di questa lezione.
Equazioni fratte di secondo grado, spiegazione
Un’equazione fratta di secondo grado nella forma normale si presenta come una frazione algebrica in cui sia al numeratore che al denominatore ci sono due polinomi. Dal punto di vista matematico questo si scrive come:
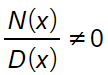
dove N(x) è il polinomio al numeratore di grado 2, mentre D(x) è un polinomio generico al denominatore.
OSSERVAZIONE: hai visto cosa ‘è al secondo membro? C’è lo zero. Questo vuol dire che per risolvere le equazioni di secondo grado fratte dovrai sempre assicurarti di passare tutto al primo membro.
Le soluzioni delle equazioni di secondo grado fratte
Quante sono le soluzioni di un’equazione fratta di grado 2? Vale lo stesso discorso fatto con le equazioni di II grado. Possono esserci cioè:
- 2 soluzioni reali e distinte
- 2 soluzioni reali e coincidenti (su alcuni libri di testo troverai scritto che c’è 1 sola soluzione)
- Non ci sono soluzioni reali.
L’unica differenza, vedremo tra poco, è nella verifica delle condizioni di esistenza, che è di fondamentale importanza nelle equazioni fratte di secondo grado.
Come si risolvono le equazioni di secondo grado fratte
Dopo questa piccola premessa veniamo all’argomento principale della lezione: come risolvere le equazioni fratte di secondo grado. Suddividiamo il procedimento risolutivo in fasi.
Passo 1 – Condizioni di esistenza
La prima cosa da fare imporre le condizioni di esistenza. Perché sono importanti? Perché un’equazione fratta di secondo grado è una frazione algebrica e quindi ha un denominatore.
Hai mai provato a fare sulla tua calcolatrice una frazione con al denominatore zero? Vedrai che la calcolatrice ti dirà che c’è un errore. Questo perché al denominatore non può esserci mai zero. In base a questa piccola considerazione, possiamo dire che le condizioni di esistenza si impongono scrivendo che ogni denominatore deve essere diverso da zero.
Generalmente queste si mettono sulla destra, così da facilitarne la lettura.
C.E.
1° denominatore ≠ 0
2° denominatore ≠ 0
…
Ogni singola condizione va risolta come se fosse un’equazione di secondo grado. Non lasciarti spaventare dal simbolo diverso, ma risolvi proprio come se ci fosse l’uguale. Per cui risolvendo le varie equazioni nelle condizioni di esistenza, si arriverà ad un risultato come:
x≠ un primo valore
x≠ un secondo valore
Alla fine dell’esercizio, andremo a verificare che le soluzioni delle equazioni di secondo grado fratte non siano uguali alle condizioni appena espresse.
Passo 2 – Ricondursi alla forma normale
Generalmente per poter passare alla forma normale delle equazioni fratte di secondo grado, cioè N(x)/D(x)=0 servono alcuni passaggi algebrici. Ricordati di:
- spostare tutto al primo membro
- calcolare il minimo comune multiplo cambiando i segni
- ridurre tutto ad un unico denominatore
- svolgere le operazioni algebriche (somme, prodotti, ecc…)
Passo 3 – Passaggio all’equazione di secondo grado
Una volta arrivato alla condizione N(x)/D(x)=0 ed imposte già le condizioni di esistenza, puoi eliminare il denominatore e risolvere semplicemente il numeratore come se fosse una normale equazione di secondo grado.
N(x)=0
Puoi scegliere il metodo che preferisci per risolvere l’equazione. Somma e prodotto, delta, delta quarti, scomposizione di polinomi, …
Come già detto a questo punto ci sono tre possibili casi:
- Δ>0 – L’equazione ha due radici reali e distinte:
x1= valore 1
x2= valore 2 - Δ=0 – L’equazione ha una sola soluzione (si dice anche che ne ha due reali e coincidenti)
x1,2= valore 1 - Δ<0 – Essendo il < title=”delta negativo” href=”https://www.esercizimatematica.com/delta-negativo-equazioni-secondo-grado/”>delta negativo, l’equazione non ha soluzioni reali.
Passo 4 – Verifica delle soluzioni
Non importa che tu abbia 1 o 2 soluzioni. E’ fondamentale verificare che queste siano compatibili con le condizioni di esistenza. Cioè verifica che i valori che ti escono nelle soluzioni siano diversi da quelli ottenuti nelle C.E.
Se dovesse esserci una o più soluzione non compatibile con le condizioni di esistenza, questa non può essere considerata accettabile. Per cui accanto ad essa andrai a scrivere soluzione non accettabile per le condizioni di esistenza. Vedremo tra poco alcuni esercizi svolti in cui ti troverai in questo caso.
Equazioni di secondo grado fratte esercizi
Esercizio 1
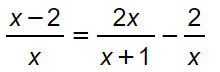
Svolgimento
La prima osservazione da fare è che non ci sono, almeno per ora, polinomi di secondo grado al numeratore. Ciò però non significa che questo esercizio non rientri tra le equazioni fratte di secondo grado, perché ci sono una serie di calcoli da fare prima di arrivare alla forma normale.
La seconda osservazione riguarda i denominatori. In questo caso non ci sono polinomi di secondo grado, per cui non sono necessarie scomposizioni. Molto spesso però sarà conveniente, per semplificare sia le condizioni di esistenza che il mcm, effettuare delle scomposizioni e ridurre i denominatori in polinomi più semplici.
Iniziamo imponendo le condizioni di esistenza. Essendo il primo e il terzo denominatore identici, non c’è bisogno di ripetere due volte che è diverso da zero.
C.E.:
x≠0
x+1≠0 → x≠-1
A questo punto posso calcolare il minimo comune multiplo tra i denominatori.
mcm: x(x+1)
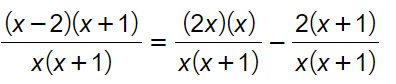
Portiamo tutto al primo membro dell’equazione, ponendo tutto sotto un’unico denominatore. Nel frattempo iniziamo già a svolgere le moltiplicazioni tra polinomi al numeratore.
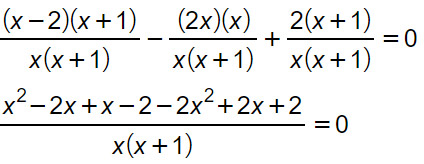
A questo punto possiamo eliminare il denominatore e fare le somme algebriche al denominatore.
-x²+x=0 → x²-x=0
x(x-1)=0
x=0 → Soluzione non accettabile con le condizioni di esistenza.
x=1
Come puoi vedere già da questo primo esercizio, la prima soluzione viola le condizioni di esistenza per cui non può essere accettata. L’unica soluzione dell’esercizio sarà x=1.
Esercizio 2
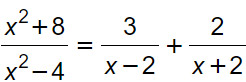
Svolgimento
In questo secondo esercizio cerchiamo di fare attenzione ai denominatori. Ci capiterà spesso, per risolvere le equazioni di secondo grado fratte, di trovare dei denominatori “sospetti”. Cosa vuol dire? Guarda la prima frazione e guarda le altre due. Ricordi la regola del prodotto di una somma per una differenza?
x²-4=(x+2)(x-2)
Quindi possiamo riscrivere l’esercizio come:
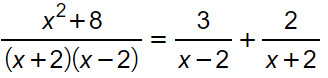
A questo punto possiamo scrivere il minimo comune multiplo:
C.E.:
x+2≠0 → x≠-2
x-2≠0 → x≠+2
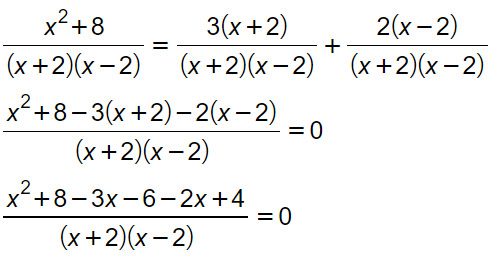
A questo punto eliminiamo il denominatore, sommiamo i termini simili e arriviamo all’equazione di II grado.
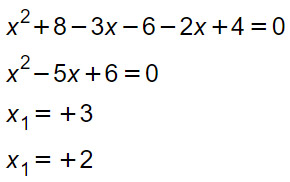
Confrontando le due soluzioni con le condizioni di esistenza, possiamo scrivere il risultato finale:
x=+2 → Soluzione non accettabile per le C.E.
x=+3
Esempio 3
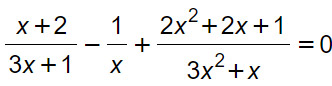
Svolgimento
Scomponiamo subito il secondo denominatore per avere:
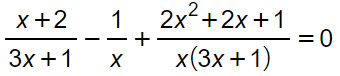
Possiamo ora determinare le condizioni di esistenza e quindi il minimo comune multiplo.
C.E.:
x≠0
3x+1≠0 → x≠-1/3
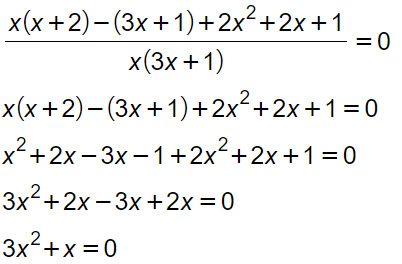
x(3x+1)=0
x=0 → Non accettabile per le C.E.
3x+1=0 → x=-1/3 → Non accettabile per le C.E.
Poiché entrambe le soluzioni violano le condizioni di esistenza, allora l’esercizio ha come risultato impossibile.
Equazioni di secondo grado fratte – esercizi da svolgere
Per continuare ad esercitarti, ti consigliamo di risolvere le equazioni fratte di secondo grado di seguito. Alcune di queste sono già state risolte negli esempi sopra.
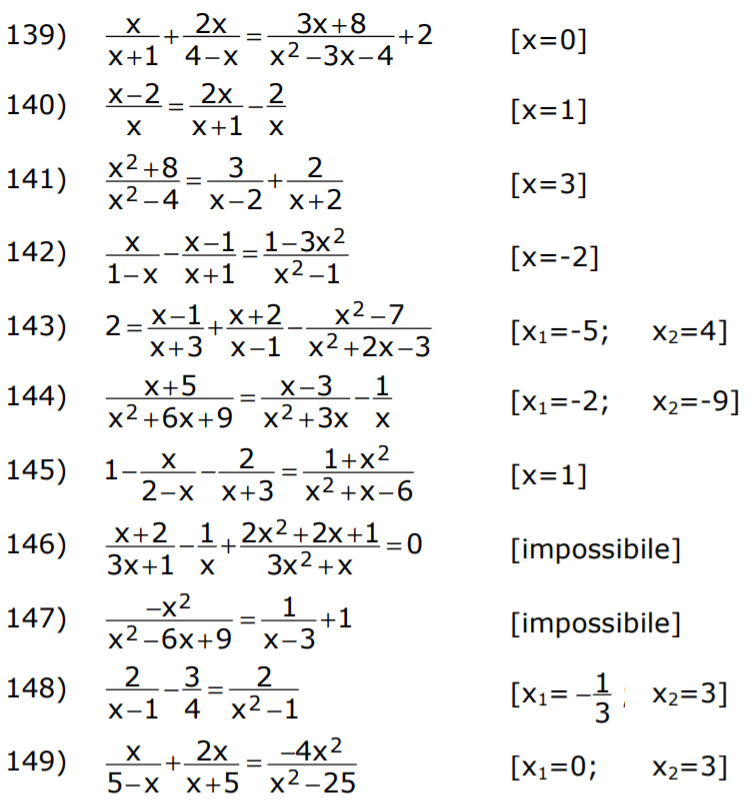
Grazie finalmente una spiegazione eccellente
Le ho capite😃
Grazie Annamaria, continua a seguirci nel proseguo dei tuoi studi e se hai altre difficoltà scrivici pure! 😉