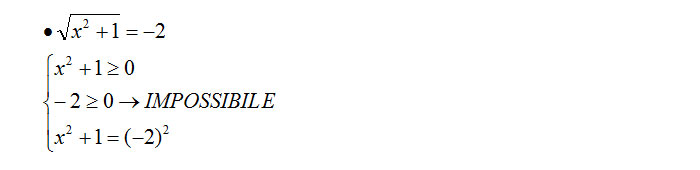Le equazioni irrazionali sono delle equazioni in cui l’incognita x compare sotto forma di radice. Come vedremo, per risolvere le equazioni irrazionali, è fondamentale guadare se l’indice di radice è pari o dispari. Distingueremo così i due casi e i differenti metodi di risoluzione.
Per rendere il tutto più completo e non trascurare nessuno dei casi più complessi analizzeremo anche le equazioni irrazionali fratte, cioè quelle equazioni con radicali anche al denominatore. A completare la lezione troverai alla fine alcuni esercizi svolti.
Per capire la spiegazione sulle equazioni irrazionali è fondamentale avere ben presente le proprietà dei radicali e come si fanno le razionalizzazioni, così da non avere problemi con le irrazionali fratte.
Cosa sono le equazioni irrazionali
Si definiscono equazioni irrazionali quelle equazioni che presentano almeno un radicale contenente un’incognita.
Questo praticamente significa che la x deve trovarsi all’interno delle radici. Ad esempio:
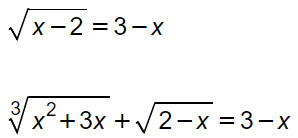
Per risolvere le equazioni irrazionali è generalmente sufficiente elevare entrambi i membri dell’equazione ad un’opportuna potenza (a proposito, ricordi le proprietà delle potenze?). Solo in questo modo potremo eliminare le radici quadrate. Non è tuttavia così immediato: prima bisogna valutare l’indice di radice.
Equazioni Irrazionali e condizioni di esistenza
Ti invitiamo a prestare attenzione ad una sola considerazione: quando ti trovi di fronte ad un equazione radicale con indice pari, ad esempio una radice quadrata, il radicando non deve mai essere negativo, altrimenti l’equazione diventa impossibile.
Non ci credi? Prova a risolvere, sulla tua calcolatrice, la radice quadrata di -2. Vedrai che la calcolatrice di dirà: ERRORE. Questo perché stai violando le condizioni di esistenza.
Tutto questo per dire che quando dovremo risolvere delle radici quadrate con indice positivo dovremo imporre il radicando maggiore o uguale di zero. Detto in parole povere, tutto quello che è sotto radice va imposto maggiore e uguale di zero.
Fatta questa doverosa premessa iniziamo con calma: gli esercizi possono presentarsi in due modi differenti:
Equazioni irrazionali con indice dispari
Se l’indice della radice è dispari, ad esempio se ho una radice cubica, non sono necessarie condizioni di esistenza. In questo caso per risolvere gli esercizi è sufficiente elevare tutto all’indice di radice.
![]()
Quindi se io ho una radice cubica che mi crea problemi, semplicemente elevo tutto alla terza senza preoccuparmi di nulla. In questo modo ottengo un’equazione razionale, molto più semplice in genere per gli studenti.
Equazioni irrazionali con indice pari
Se l’indice di radice è pari, oltre ad elevare a potenza, sono necessarie le condizioni di esistenza. Dovremo quindi imporre entrambe le funzioni maggiori di zero.
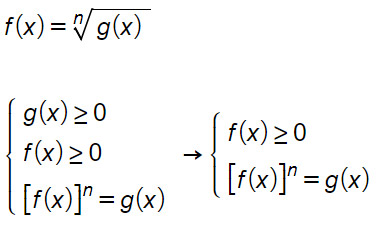
Come puoi osservare tu stesso devo risolvere un sistema di disequazioni. La prima disequazione non è altro che la condizione di esistenza della radice. La seconda è dovuta alla concordanza del segno tra i due membri.
Tuttavia la prima disequazione del sistema può essere omessa perché se f(x)≥0 e allo stesso tempo f(x)n=g(x), allora implicitamente anche g(x)≥0. L’ultima equazione è stata semplicemente ottenuta elevando a potenza.
Alcuni consigli per risolvere le equazioni irrazionali
Come hai potuto vedere, si tratta di una tipologia di esercizio non particolarmente difficile, ma è fondamentale fare attenzione a seguire il metodo risolutivo per evitare alcuni errori. Il più comune commesso dagli studenti durante i compiti è il seguente:
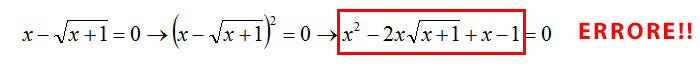
Perché questo esercizio è sbagliato? Perché non è stata isolata la radice al primo membro. Quando vado ad eseguire l’elevazione a potenza, ottengo un quadrato di binomio e, con il doppio prodotto, la radice non va via. Il modo migliore per risolvere questa equazione irrazionale è invece:
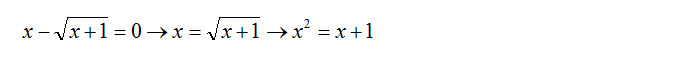
Oltre a ciò dovremo ovviamente ricordarci di impostare il sistema di disequazioni.
Equazioni Irrazionali con due radicali
Non cambia assolutamente nulla rispetto ai casi precedenti.
- Se l’indice è dispari, basta fare un’elevazione a potenza di entrambi i membri – ricordiamo ovviamente di tenerne uno a destra e uno a sinistra.
- Se l’indice è pari si scrive il sistema come in precedenza. Entrambe le disequazioni del sistema, però, stavolta sono dovute alle condizioni di esistenza. A livello pratico non ci cambia niente: scrivo un sistema con entrambi i radicandi maggiori di zero e all’ultimo rigo l’equazione irrazionale elevata a potenza.
Esercizi svolti sulle equazioni irrazionali
Verifichiamo che le seguenti disequazioni irrazionali siano impossibili.
Esercizio svolto -1
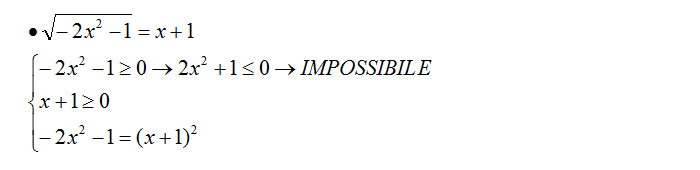
La condizione di esistenza, ovvero la prima disequazione di secondo grado è impossibile! Il binomio 2 x al quadrato più 1 deve essere necessariamente maggiore di zero.
Esercizio svolto -2
Questa volta l’esercizio è impossibile perché il secondo membro è minore di zero.
Cambiamo ora tipologia e vediamo assieme come risolvere gli esercizi sulle equazioni irrazionali.
Esercizio svolto -3
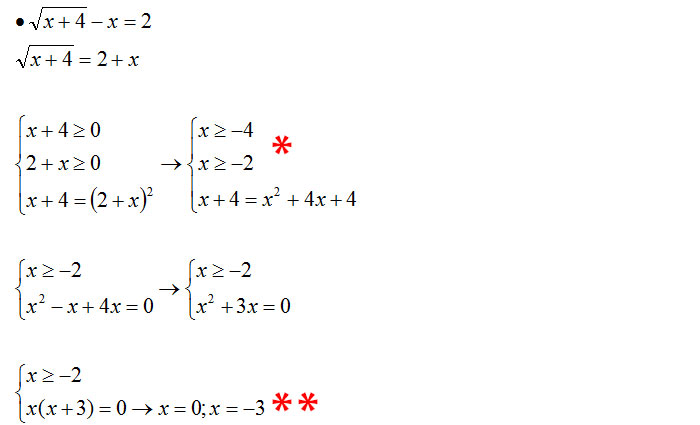
* Se x deve essere maggiore o uguale di -2 (dalla seconda disequazione), allora sicuramente è maggiore o uguale di -4. Per cui La prima disequazione posso anche evitare di riportarla.
** Le due soluzioni sono accettabili? Confronta sempre i risultati dell’equazione con quelli delle disequazioni. Quest’ultima infatti ci ricorda che la x deve essere maggiore o uguale di -2. Questo significa che x=-3 non è una soluzione accettabile. L’unica soluzione accettabile è x=0.
Esercizio svolto -4
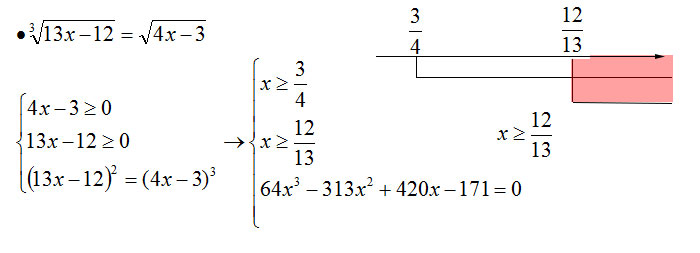
Imponiamo come sempre per gli esercizi sulle equazioni irrazionali la condizione di esistenza per il radicale pari (prima disequazione), la concordanza del segno con l’altro membro (seconda disequazione) ed infine eleviamo per il minimo comune multiplo tra 2 e 3 (gli indici di radice). Cioè eleviamo tutto alla potenza 6. Noterai che al primo termine devo risolvere un quadrato di binomio, mentre al secondo termine svolgo il cubo di binomio.
Risolviamo il sistema di due disequazioni scrivendo i risultati sul grafico per ottenere x maggiore e uguale di 12/13. Proseguiamo eseguendo i calcoli risolvendo l’equazione di terzo grado attraverso il metodo di Ruffini.
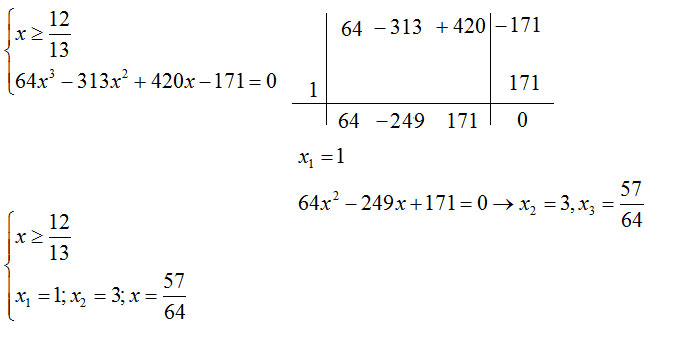
Per poter essere valida la condizione di esistenza, cioè la disequazione al primo rigo, sono valide solo due soluzioni, cioè x=1 e x=3.
Ti lasciamo con alcuni esercizi sulle equazioni irrazionali che puoi risolvere da solo. Se invece hai ancora dei dubbi o se la lezione ti è stata utile e vuoi aiutarci a crescere, lascia un commento alla fine della lezione.
Equazioni irrazionali esercizi da svolgere