Qual è la formula del delta? Come si calcola il delta delle equazioni di secondo grado in modo semplice? Potreste indicarmi anche la formula del delta quarti e qualche esempio su come utilizzarle? Grazie – Giacomo
Al nostro lettore Giacomo e a tutti gli studenti che vogliono sapere come si calcola il delta, proponiamo immediatamente la formula, così da rispondere subito alla domanda. Ecco come calcolare il delta:
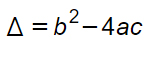
La formula del delta è: il quadrato del coefficiente di primo grado (b2) meno il quadruplo del prodotto del coefficiente di secondo grado per il termine noto (4ac).
Quindi detto in termini generici, data l’equazione di secondo grado generica
![]()
per il calcolo del delta basta elevare al quadrato il numero che si trova al posto della b e fare la differenza con il termine a la c moltiplicate per 4.
A cosa serve il calcolo del delta
Una volta calcolato il discriminante si ottiene un numero. Qui si presentano 3 casi.
- Δ>0 → l’equazione ha 2 soluzioni reali e distinte.
- Δ=0 → l’equazione ha 2 soluzioni reali coincidenti. Se provi a scomporla vedrai che otterrai un quadrato di binomio.
- Δ<0 → l’equazione è impossibile nel campo dei numeri reali. Leggi l’approfondimento sulle equazioni con delta negativo.
Appare quindi evidente la funzione del delta: indicarci se esistono e quante sono le soluzioni dell’equazione studiata. Si può inserire la formula del delta all’interno della formula risolutiva delle equazioni di secondo grado.
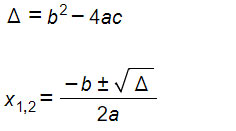
Esempi su come si applica la formula del delta
Esercizio 1)
3x2+7x+2=0
Si voglia in questo esercizio solo applicare la formula del delta senza trovare le soluzioni dell’equazione. Per prima cosa individuiamo i coefficienti:
a=3, b=7, c=2
Δ=b2-4ac=
=72-4(3)(2)=
=49-24=25
In questo caso il delta è un numero maggiore di zero, per cui esistono due soluzioni reali e distinte.
Esercizio 2)
x2+2x+√3=0
Come prima applichiamo la formula del delta trovando i coefficienti da inserire:
a=1, b=2, c=√3
Δ=b2-4ac=
=22-4(1)(√3)=
=4-4√3.
Il delta è sempre un numero positivo ma ha la particolarità di contenere una somma con una radice. Andando a calcolare poi le soluzioni dell’equazione ci troveremo con una radice con all’interno un’altra radice. L’unico modo che abbiamo per risolverla è utilizzare la formula dei radicali doppi quadratici. Lasciamo tuttavia la conclusione di questo esempio a te: sarà un ottimo modo per esercitarti.
Formula delta quarti
Si utilizza praticamente solo al secondo anno della matematica delle scuole superiori perché rappresenta un formula aggiuntiva da imparare che può essere sostituita perfettamente dalla formula del delta vista fino a questo momento. Abbiamo dedicato un’intera lezione al delta quarti e alla formula ridotta.
Riepilogando in breve: si utilizza quando il coefficiente del termine di primo grado è un numero pari. Serve sostanzialmente per ridurre quelle espressioni in cui i numeri sono molto gradi. La formula del delta quarti è la seguente:
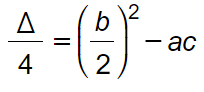
La formula per calcolare il delta quarti prevede di dividere a metà il coefficiente del termine di primo grado e poi elevarlo al quadrato. Al numero che si ottiene bisogna sottrarre il prodotto tra il coefficiente del termine di secondo grado e il termine noto.
Esempio di applicazione formula delta quarti
x2+4x+3=0
Individuiamo come sempre i coefficienti: a=1, b=4, c=3.
Δ/4=(b/2)2-ac=
=(4/2)2-(1)(3)=
=4-3=1
Anche in questo caso la formula del delta quarti ci fornisce un risultato positivo, per cui l’equazione di secondo grado avrà due soluzioni reali e distinte.
Consigli e conclusioni
Ora sai tutto quello che c’è da sapere sulla formula del delta. Ti consigliamo di impararla a memoria anche perché la utilizzerai molto spesso. Il nostro consiglio, per memorizzarla più velocemente è di fare tanti esercizi e ogni volta di ricopiarti la formula del delta. Vedrai che dopo 2 o 3 esercizi la ricorderai già a memoria.