Il prodotto di somma per differenza è il primo e il più semplice dei prodotti notevoli che consente di moltiplicare tra loro due binomi con caratteristiche simili risparmiando tempo ed inutili passaggi.
La formula per calcolare il prodotto di una somma per una differenza è:
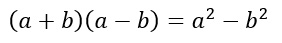
DEFINIZIONE: Il prodotto di una somma per una differenza è uguale alla differenza dei quadrati dei monomi di partenza.
Di seguito trovi la video-lezione che abbiamo registrato per te su youtube. Puoi guardare il video oppure continuare con la lettura per trovare le regole con altri esercizi svolti.
Questa regole può essere applicata anche con parentesi di 3 elementi, infatti vedremo in uno degli esempi come si svolge la somma per differenza di trinomio. Facciamo però le cose con calma e iniziamo a capire perché si utilizza questa formula invece di ricorrere alle classiche moltiplicazioni tra polinomi.
Somma per differenza binomio – la dimostrazione
Dobbiamo eseguire la moltiplicazione tra binomi (a+b)(a-b). Risolviamo riportando tutti i passaggi:
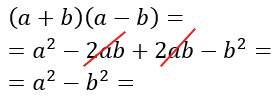
Come puoi vedere i termini centrali si eliminano, per cui si ottiene sempre la differenza di due termini al quadrato.
L’unica difficoltà di questo prodotto notevole sta nel saper riconoscere i due elementi di partenza che devono essere perfettamente uguali tranne che per un segno.
Somma per differenza trinomio
In base a quanto appena detto possiamo estendere il ragionamento anche ai trinomi: l’importante è che i due trinomi che si moltiplicano siano identici ad eccezione di un unico segno.
La formula in questo caso è del tipo:
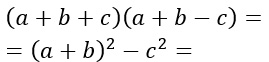
I termini uguali vengono quindi posti al quadrato (per non sbagliare utilizziamo delle parentesi) segue il segno meno e l’ultimo monomio, ovvero c, alla seconda. La potenza tra parentesi è un quadrato di binomio, se però non hai ancora studiato la regola, risolvi il tutto come se fossero delle normali moltiplicazioni di trinomi.
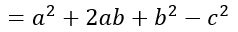
Il suo uso nelle scomposizioni
La regola del prodotto di somma per differenza viene molto utilizzata anche nell’ambito delle scomposizioni di polinomi: basta semplicemente leggere la formula da destra verso sinistra.
In parole povere, ne parleremo poi nella lezione di approfondimento dedicata alla differenza di quadrati, vale anche la regola:
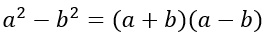
Cioè la differenza di due quadrati può essere riscritta come la moltiplicazione di somma per differenza di binomi.
Esercizi somma per differenza
ESERCIZIO 1
Svolgere la seguente moltiplicazione di binomi
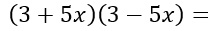
In questo primo esercizio svolgiamo davvero tutti i passaggi, così da ripetere in maniera davvero semplice la regola appresa. Abbiamo visto che il passo fondamentale è riconoscere di essere di fronte a due polinomi uguali tranne che per un segno.
In questo caso il primo monomio è lo stesso, poiché abbiamo 3 sia nella prima parentese che nella seconda. Gli altri due monomi invece (+5x e -5x) sono opposti, cioè hanno segno differente ma numero e parte letterale uguale.
Per cui possiamo applicare la formula del prodotto di una somma per una differenza: quadrato del primo monomio meno quadrato del secondo monomio.
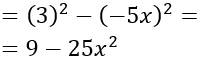
ESERCIZIO 2
Svolgere il seguente prodotto di somma per differenza di binomi:
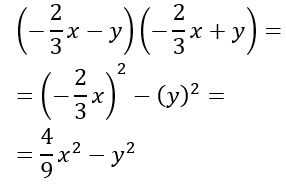
Come puoi vedere in questo esercizio svolto, la presenza di ulteriori segni non crea nessun tipo di variazione. L’importante è che le due parentesi che si moltiplicano siano perfettamente uguali ad eccezione di un unico segno.
ESERCIZIO 3
Risolvere la somma per differenza di un trinomio:
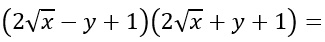
L’unico segno che cambia in questa moltiplicazione è quello della y. Mettiamoci in ordine i vari monomi così che i primi due siano quelli il cui segno resta invariato:
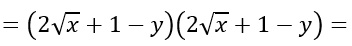
Eseguiamo il quadrato del blocco di elementi uguali meno il quadrato dell’ultimo, cioè y.
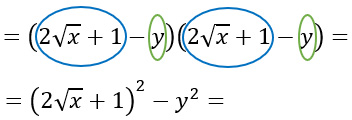
A questo punto sviluppiamo il quadrato del primo binomio e siamo arrivati rapidamente alla soluzione.
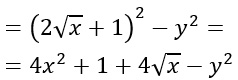
Conclusioni
Abbiamo quindi visto come risolvere il prodotto notevole somma per differenza in maniera semplice e veloce. Abbiamo imparato assieme che grazie a questa regola possiamo velocizzare lo svolgimento delle nostre espressioni algebriche.
Se questa lezione ti è stata utile o se hai altri dubbi o domande, lascia un commento in basso. Ci consentirà di migliorare la qualità delle nostre lezioni. Buono studio!
Grazie, la spiegazione e gli esercizi mi sono stati utili e adesso vado come una scheggia ! 😉
Grazie Gabriele, continua a seguirci 😉 e per qualsiasi problema in matematica, noi ci siamo!