La divisione tra polinomi si esegue attraverso una tecnica basata su pochi semplici passaggi che portano rapidamente a calcolare quoziente e resto. In questa lezione vedremo come si fa la divisione tra polinomi con una spiegazione passo-passo, così da rendere il tutto più semplice e chiaro per lo studente.
Per comprendere questa lezione, soprattutto la parte che riguarda le lettere, è importante conoscere le proprietà delle potenze. In particolare, quando divido due elementi con coefficienti letterali, gli esponenti si sottraggono. Vedremo comunque meglio negli esercizi questo aspetto.
La regola generale da tener presente per calcolare la divisione di polinomi è:
A(x):B(x)=Q(x)×B(x)+R(x)
Quindi facendo dividendo i due polinomi A e B si ottiene il polinomio Q detto quoziente a cui va moltiplicato il divisore B e si somma infine il resto R. Vediamo nella pratica come si fanno i calcoli.
Divisioni tra polinomi e monomi
La divisione polinomiale più semplice riguarda un polinomio da dividere per un monomio. In questo caso semplicemente semplicemente si applica la proprietà distributiva della divisione. Così come siamo stati abituati con le moltiplicazioni tra polinomi, è sufficiente dividere ciascun termine del polinomio per il monomio.
Esempio 1
Vediamo subito un esempio su come si fa la divisione:
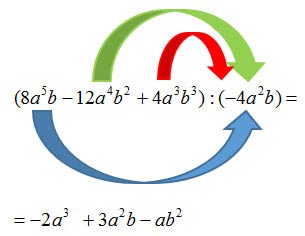
COME LO ABBIAMO RISOLTO:
- Il primo termine del polinomio va diviso per il monomio divisore → (8a5b) : (-4a²b) = -2a³
- Si passa a questo punto al secondo termine → (-12a4b2 ) : (-4a²b) = +3a²b
- Si divide l’ultimo termine del polinomio → (4a³b³): (-4a²b) = -ab²
Esempio 2
In un secondo esercizio vediamo come si fanno le divisioni tra polinomi con frazioni. Non cambia nulla, per risolvere eventuali somme è importante solo che tu ricordi come si calcola il minimo comune multiplo.
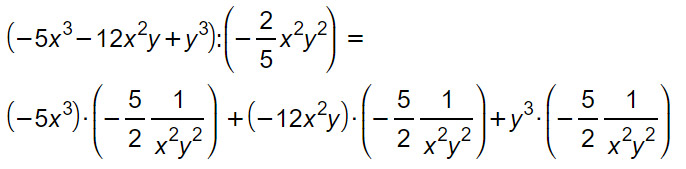
Come puoi vedere, nel caso in cui ci siano delle frazioni, il divisore B si riscrive invertendo numeratore e denominatore. In pratica vale la regola:
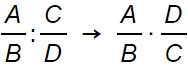
Per cui proseguendo con i calcoli si possono fare delle semplificazioni fino a scrivere:
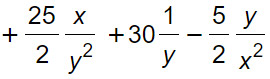
E’ importante, quando devi risolvere un esercizio con le frazioni, che fai prima la divisione tra i segni, poi tra i numeri (abbiamo visto nella lezione sulle operazioni tra numeri relativi che si trasforma in divisione “capovolgendo” il divisore) e infine le lettere.
Divisione di polinomi: spiegazione passo passo
Questa regola possiamo dividerla in due parti: le divisioni tra polinomi con resto e senza resto. Si procede innanzitutto ordinando il polinomio in base al suo grado secondo le potenze decrescenti. Vediamo un esempio assieme commentando passo passo:
![]()
Entrambi i polinomi sono già ordinati secondo le potene decrescenti di a. Si inizia dividendo il primo termine del dividendo (cioè 6a al cubo) per il primo del divisore (-3a al quadrato). Aiutiamoci con delle frecce:
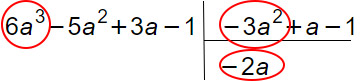
OPERAZIONI SVOLTE:
6a³ : (-3a²) = -2a
Il risultato della prima operazione va in basso a destra (-2a) e fa parte del quoziente, cioè del risultato finale da ottenere. A questo punto moltiplichiamo questo valore ottenuto (-2a) per i tre monomi del divisore (-3a al quadrato +a e -1) e il risultato lo scriviamo sulla sinistra (cambiato di segno) sotto il polinomio (attenzione a mettere ben in colonna i termini con lo stesso grado).
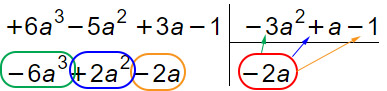
OPERAZIONI SVOLTE
- (-2a) · (-3a²) = +6a² → cambio il segno → -6a²
- (-2a) · (+a) = -2a² → cambio il segno → +2a²
- (-2a) · (-1) = +2a → cambio il segno → -2a
A questo punto sommo algebricamente i termini in colonna delle due righe, per ottenere:
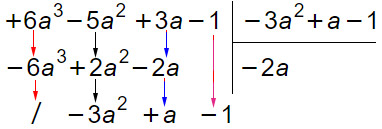
OPERAZIONI SVOLTE
- +6a³-6a³ = 0
- -5a²+2a²=-3a²
- +3a-2a=+a
- Riporto il -1 nell’ultima riga.
Piccolo trucchetto per risolvere le divisioni: il primo termine risultante dalla somma algebrica sia sempre pari a 0! Se non dovesse trovarsi, c’è qualche errore!
A questo punto si riparte nuovamente come dall’inizio. Cioè si divide il primo termine del nuovo polinomio (-3a al quadrato) per il primo termine del polinomio divisore (-3a al quadrato) … Prosegui da solo e vedrai che alla fine il risultato che otterrai sarà:
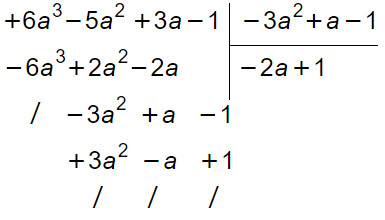
Per cui il quoziente Q=-2a+1, mentre il resto R=0.
Come puoi vedere dalla figura il resto della divisione tra polinomi in questo caso è zero. Se avessimo trovato qualche monomio nella colonna di sinistra allora il resto sarebbe stato diverso da zero. In questo caso la divisione si dice esatta proprio dà resto nullo.
Esercizio svolto
Quella che stiamo per risolvere assieme è una divisione tra polinomi con coefficienti letterali. Ricordati che una delle tue lettere è l’incognita (nel nostro esempio a) mentre l’altra va trattata come se fosse semplicemente un numero. Vediamo come si risolve la divisione tra questi due polinomi:
(a4+a4):(a+b)
SVOLGIMENTO
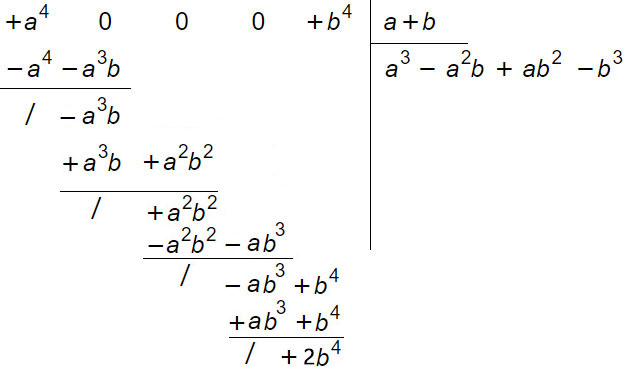
Due cose importanti che non abbiamo ancora specificato:
- E’ necessario, come detto, mettere in ordine il polinomio con grado decrescente. La cosa importa è che se il grado manca, come nell’esempio, occorre mettere uno 0. Senza questo trucchetto, la regola delle divisioni tra polinomi non funziona e il risultato darà sempre errore.
- Quando finisce la divisione? La divisione tra polinomi finisce quando nello spazio riservato al resto c’è un monomio (o un polinomio) con grado inferiore al divisore. In questo caso è uscito -b alla quarta. Considerato che il polinomio è ordinato in base alla lettera, il grado è quindi 0. Minore del grado del divisore (a+b) che rispetto alla lettera a ha grado 1. Per cui la divisione finisce qui.
Volendo fare la prova della divisione appena svolta è necessario moltiplicare il quoziente per il divisore e si somma a questo il resto: si deve ottenere il dividendo.
Un modo alternativo per risolvere le divisioni tra polinomi è con Ruffini. Analizzeremo tuttavia il metodo di Ruffini in un’altra lezione. Per ora è preferibile continuare a fare pratica con qualche esercizio sulle divisioni tra polinomi.
Esercizi da risolvere
Eseguire le seguenti divisioni:
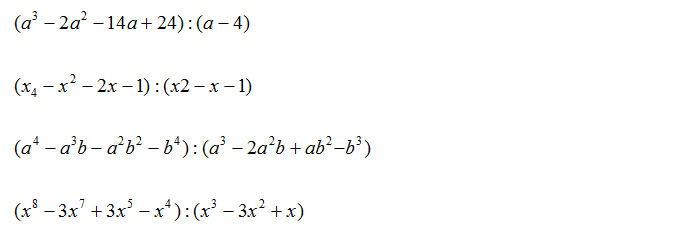
Vuoi esercitarti ancora? Ecco alcuni semplici esercizi tra polinomi semplici proposti dall’Università di Bologna. Se hai dubbi o se non riesci a risolvere gli esercizi di matematica che ti sono stati assegnati puoi contattarci. Siamo qui per aiutarti.
Gli esercizi proposti dagli studenti
 In questo file abbiamo raccolto gli esercizi più difficili sulle divisioni di polinomi che ci sono stati segnalati dagli studenti. Sono risolti e commentati passo passo. Buon lavoro.
In questo file abbiamo raccolto gli esercizi più difficili sulle divisioni di polinomi che ci sono stati segnalati dagli studenti. Sono risolti e commentati passo passo. Buon lavoro.
Grazie mille…. Utilissimo!!!!!
Nell’esempio con le frecce colorate secondo me c’è un errore: nella prima divisione la parte letterale b si annulla e quindi non deve comparire nel risultato.
Grazie Renato, abbiamo già provveduto a sistemare l’errore. Continua a seguirci.
Eccellente, veramente precisi e chiari. Grazie
C’é un errore nella “Regola da tener presente”, é piú che altro formale, ma comunque importante: Lí c’é scritto A(X):B(X)=Q(X)+R(X)*B(X) ed é sbagliato se intendiamo Q(X) come polinomio quoziente e R(X) come polinomio di resto. La forma “corretta” é A(X):B(X)=Q(X)*B(X)+R(X)
Grazie Davide,
abbiamo già provveduto a correggere il testo. Siamo sempre orgogliosi quando i nostri lettori/studenti intervengono per migliorare gli appunti messi a disposizione.
Continua a seguirci 😉
NON CAPISCO IL SECONDO ESEMPIO (a4+b4):(a+b). Secondo me lo avete sbagliato. Potreste risolverlo tutto ?
Ciao Giovanni, c’era un refuso con un segno. Ora l’esercizio è stato corretto. Grazie per la segnalazione e buono studio.