Calcolo letterale esercizi svolti e teoria semplificata

Fino a questo momento abbiamo studiato il calcolo letterale applicato a problemi geometrici. In realtà la matematica non è fatta di soli numeri, ma anche di formule, lettere e simboli. Oggi vedremo un’introduzione al calcolo letterale.

---

Gli argomenti della lezione

• Introduzione al calcolo letterale
• Perché imparare a fare i calcoli con le lettere?
• Operazioni con le lettere
• Esercizi svolti e da risolvere

---

Introduzione al calcolo letterale

Nella scorsa lezione abbiamo visto le espressioni algebriche con i numeri relativi, applicando, se necessario le proprietà delle potenze. Oggi inizieremo ad anticipare il calcolo letterale di monomi e polinomi.

Perché fare il calcoli con le lettere?

Le espressioni algebriche che abbiamo imparato a risolvere non sono fatte solo di numeri, ma anche di lettere. Il calcolo letterale in geometria è fondamentale. Quando noi diciamo che l’area di un rettangolo si calcola base per altezza, vuol dire che possiamo scrivere:

Arettangolo=b x h

Questa altro non è che un’espressione algebrica con le lettere. Non dobbiamo quindi meravigliarci che, anche in algebra quindi, i nostri esercizi siano fatti di numeri ma anche di lettere.

Per rispondere alla domanda “il calcolo letterale a che serve?” possiamo solo solo dire per ora che sarà fondamentale nello studio delle equazioni che vedremo più avanti: in generale il calcolo letterale serve a permetterci di calcolare qualcosa che ancora non si conosce, cioè un’incognita. Ma studieremo bene questo aspetto nelle prossime lezioni.

Calcoli algebrici e operazioni con le lettere

Ripassiamo assieme le operazioni con i numeri relativi usando questa volta le lettere.

+a-a=0

 

Se su una scrivania vuota io metto una penna, quindi sommo un determinato elemento e subito dopo la tolgo, chiaramente la scrivania resterà vuota. Questo significa che se ho una lettera, prima sommata e poi sottratta, il risultato sarà nullo, cioè 0.

+a+(+b-c)=+a+b-c

Se ho un segno “più” davanti ad una parentesi e al suo interno non ci sono operazioni da svolgere, posso rimuovere semplicemente la parentesi.

+a-(+b-c)=+a-b+c

Diverso è il caso in cui davanti una parentesi ho il segno meno. In questo caso, mai dimenticarlo, è necessario rimuovere la parentesi e cambiare tutti i segni all’interno.

(+a) x (+b) = +ab

Per moltiplicare due lettere tra loro diverse, semplicemente si accostano l’una accanto all’altra, moltiplicando i segni con la regola dei segni già vista nelle scorse lezioni nelle operazioni con i numeri relativi.

Questo implica anche che, ogni volta che troviamo due lettere vicine in un’espressione algebrica, queste sono tra loro moltiplicate. Essendo valide le regole dei segni, posso anche scrivere.

(-a) x (+b) = -ab

(-a) x (-b) = +ab

(+a) x (-b) = -ab

Per quanto riguarda le potenze, posso inoltre scrivere che se l’esponente è pari allora il segno meno può essere eliminato:

(-a)ⁿ=aⁿ

 Se invece l’esponente è dispari è allora il segno rimane.

(-a)ⁿ=-aⁿ

Valgono inoltre le cinque proprietà delle potenze già viste nella scorsa lezione.

aⁿ x a^m= a^m+n

aⁿ : a^m= a^m-n

(aⁿ)^m= a^mn

a^m : b^m= (ab)^m

a^m : b^m= (a:b)^m

Calcolo letterale, esercizi svolti e da svolgere

Generalmente teniamo separata la parte teorica da quella pratica. Tuttavia questa lezione di matematica, in fondo, non è stata altro che un ripasso di quanto già appreso precedentemente. Essendo stata molto rapida possiamo quindi passare immediatamente alle esercitazioni, iniziando come sempre da esercizi di calcolo letterale svolti.

(2a+b)³ -2(a+b)² 

dove a=-1/2;  b=-1

Questi tipi di esercizi sul calcolo letterale sono particolarmente semplici. E’ sufficiente sostituire alla lettera il valore indicato sulla destra per ottenere una semplice espressione algebrica numerica.

Consiglio: quando andiamo a sostituire, ricordiamoci di inserire una parentesi nei valori inseriti. Ecco come…

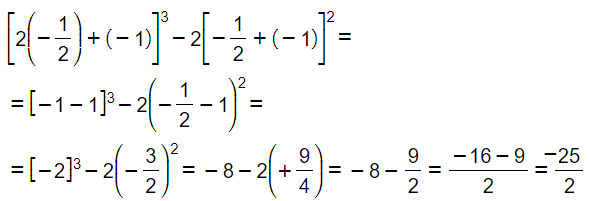
Ora proviamo a risolvere il calcolo letterale con una sola variabile, ovvero con una sola lettera. Sarà, ovviamente ancora più semplice:

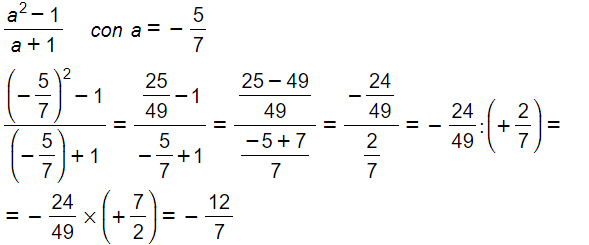
Di seguito vi proponiamo un elenco di esercizi con cui poter fare pratica con l’argomento.

Attenzione quando al denominatore c’è il numero 0

L’ultimo esercizio, il n.224, lo abbiamo già svolto insieme. Il testo sottolinea anche come per a=-1 il risultato sia impossibile. Vi siete già fatti un’idea del perchè?

Se non sapete rispondere a questa domanda vi consiglio di prendere la vostra calcolatrice e di provare a fare una divisione tra due numeri. Il secondo deve essere 0. Ad esempio: sette diviso zero – non fatelo a mente – cosa dice la calcolatrice? ERRORE!

Questo perché è impossibile risolvere una divisione quando al denominatore c’è 0. Questa è una regola fondamentale che approfondiremo meglio quando parleremo di condizioni di esistenza, sia negli esercizi sulle equazioni che sugli esercizi di analisi del V anno.

Per ora ci basti sapere che un divisione non può mai avere al denominatore lo 0.

Se siete riusciti a risolvere tutti gli esercizi, vi invitiamo a procedere con il prossimo capitolo. Appreso come risolvere i problemi con il calcolo letterale, possiamo finalmente passare alle proprietà e regole sui monomi.

Se invece persistono problemi o dubbi sul calcolo letterale, vi invitiamo a contattarci, restiamo come sempre a vostra disposizione.