La regola di Ruffini viene utilizzata in algebra per la divisione di un polinomio per un binomio di primo grado con la forma (x-a) o (x+a).
![]()
Ad esempio:
![]()
Con il metodo di Ruffini, oltre alla divisione è possibile anche eseguire in maniera più agevole la scomposizioni di polinomi, soprattutto se questi hanno un grado superiore al secondo. Ne parleremo in una lezione specificamente dedicata alla scomposizione con Ruffini.
Come applicare la regola di Ruffini
PREPARA IL POLINOMIO DIVIDENDO
La prima cosa da fare è ordinare il polinomio con gli esponenti in modo decrescente. Parti dal grado massimo e vai a scendere. Nel caso in cui manca una potenza, ricordati che sul grafico, al suo posto, dovrai mettere 0.
DISEGNA UNA PICCOLA TABELLA
Proviamo ad esempio a risolvere proprio la divisione che abbiamo visto in alto e facciamolo commentando ogni singolo passaggio.
Qui andremo a scrivere tutti i coefficienti, ovvero la parti numeriche, dei monomi che compongono il polinomio da dividere. Come già anticipato, ogni volta che manca una potenza, inserirai al suo posto uno 0. Ricordati infine che il termine noto del polinomio (ovvero il numero che non è accompagnato alla x) va messo all’esterno.
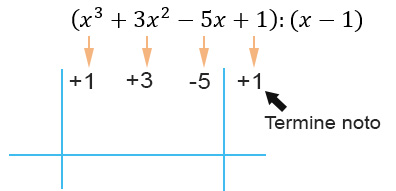
Nella parte bassa, sulla sinistra del grafico mettiamo il numero del binomio divisore cambiandogli il segno:
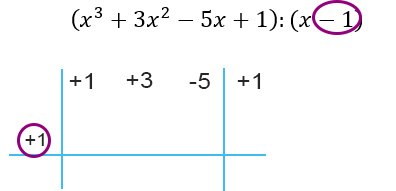
Iniziano a questo punto i calcoli veri e propri della divisione con Ruffini.
SI PORTA IL PRIMO COEFFICIENTE IN BASSO mantenendo il suo segno originale.
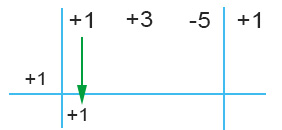
LA MOLTIPLICAZIONE: Si moltiplica il numero della riga in basso per il divisore. Il risultato lo si mette nella parte centrale del grafico nella colonna successiva.
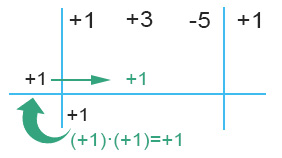
ADDIZIONE DEI TERMINI IN COLONNA: possiamo fare la somma algebrica tra i due numeri. In questo caso abbiamo nella stessa colonna +3 e +1.
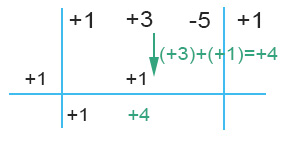
MOLTIPLICAZIONE COL DIVISORE: ripetiamo la moltiplicazione fatta 2 passaggi prima. Quindi il numero appena calcolato (+4) va moltiplicato per il divisore posto sulla sinistra (+1). Il risultato lo inseriamo nella riga centrale (+1)(+4)=+4
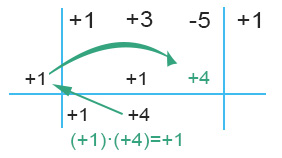
ADDIZIONE IN COLONNA: ancora una volta sommiamo algebricamente – quindi tenendo conto dei segni – i due numeri situati sulla stessa colonna.
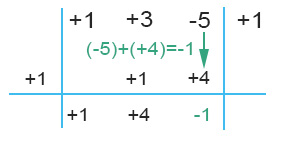
MOLTIPLICAZIONE CON IL DIVISORE: poiché siamo arrivati alla fine della nostra tabella, moltiplichiamo per l’ultima volta con il divisore per cui eseguiamo (-1)(+1)=(-1) che andremo a riportare sotto il termine noto.
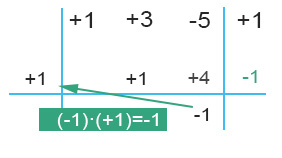
ADDIZIONE E CALCOLO DEL RESTO: sommando l’ultima colonna otteniamo il resto. In questo caso (+1)+(-1)=0 il resto è nullo.
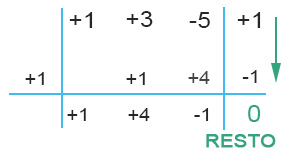
NOTA: Nel caso in cui il resto sia zero, allora il divisore che abbiamo segnato a sinistra, cioè +1, si chiama zero del polinomio. Cioè vuol dire che andando ad inserire +1 al posto della x nel polinomio di partenza, il risultato è 0. Questo sarà molto importante nelle scomposizioni con Ruffini di cui si occuperemo in seguito e utilizzeremo quello che viene proprio chiamato come Teorema di Ruffini.
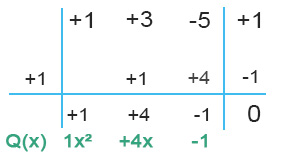
IL RISULTATO FINALE: i numeri in basso, posti sotto la riga centrale, sono i coefficienti del quoziente Q(x). Come si procede? Considera il grado del polinomio di partenza, in questo caso 3, visto che c’è un x al cubo, e abbassalo di 1.
Quindi da x al cubo (di grado 3 di partenza), mi ritrovo ora a x al quadrato (di grado 2 perché ho abbassato di 1 il grado).
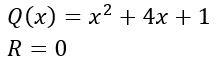
Divisione con Ruffini – esercizi
Svolgiamo qualche altro esercizio con il metodo di Ruffini così da fare un po’ di pratica assieme.
Esercizio 1
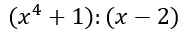
Il dividendo, ovvero il polinomio a sinistra, è composto da soli due termini. Come puoi notare mancano gli elementi di grado 3, 2,1, visto che non sono presenti x al cubo, x al quadrato e x.
Costruiamo quindi il grafico previsto dal metodo di Ruffini mettendo 0 al posto dei termini mancanti. Sulla sinistra mettiamo il divisore cambiato di segno: poiché c’è (x-2), il divisore diventa +2. Iniziamo subito portando il primo termine in basso.
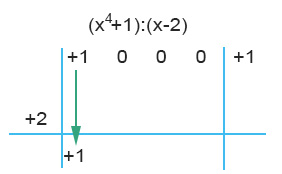
A questo punto moltiplichiamo il +1 che abbiamo portato in basso con il divisore +2 e il risultato lo mettiamo al centro. (+1)(+2)=+2
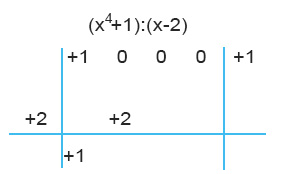
Eseguiamo la somma algebrica tra i termini in colonna: 0+2=+2
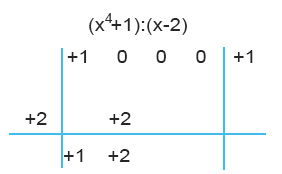
Ripetiamo la moltiplicazione, quindi (+2)(+2)=+4 e lo riportiamo al centro dello schema.
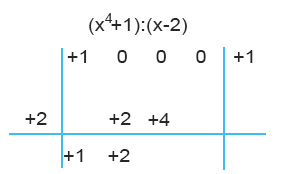
Eseguiamo la somma tra 0 e +4 in colonna: il risultato è +4.

Moltiplichiamo ora (+4) per il divisore (+2)= +8

Sommiamo ancora una volta i termini in colonna:0+8=8.

Moltiplichiamo per l’ultima volta (+8)(+2)=+16. Sommandolo con il termino in colonna +1, otteniamo il resto.

Quindi dalla nostra divisione con Ruffini abbiamo ottenuto che il resto è uguale a +17, mentre invece il quoziente è:
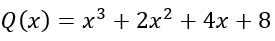
Se questa lezione ti è stata utile e siamo riusciti a chiarire i tuoi dubbi o se hai qualche problema di cui vuoi parlarci, lasciaci un commento in basso. Ci aiuterai a crescere e a migliorare la qualità delle lezioni.
quando e perché si mettono gli zeri? non ho ben capito questa parte…
Ciao Ary, gli zeri si mettono quando non è presente uno dei gradi della x. Mi spiego meglio:
verifica sempre, partendo dal termine di grado massimo, che siano presenti tutti le potenze della x a decrescere.
Per esempio:x^4+5x^2+3=0, come puoi vedere manca il termine al cubo e il termine di grado 1. Questo significa che sul grafico andrai ad inserire gli zeri al loro posto. Cioè inserirai come coefficienti: 1 0 5 0 3.
è un blog fantastico, complimenti da un 59enne, ex liceo scientifico ed ex economia e commercio vecchio ordinamento. mi sta venendo una voglia pazza di rispolverare le vecchie nozioni ricevute da adolescente e, ne ho la quasi certezza, penso che ce ne siano tanti in giro di miei coetanei in situazione simile con stessa voglia. Chissà, magari potrebbe essere in qualche modo un bisogno istintivo di ricordare la propria giovinezza.