Grado di un polinomio complessivo e rispetto a una lettera

Il concetto di grado di un polinomio è fondamentale per imparare a risolvere e riconoscere le equazioni in modo corretto. Viene anche detto grado del polinomio e rappresenta il grado massimo dei monomi presenti.

Si tratta di un argomento che mette spesso in difficoltà gli studenti perché non capiscono se il grado massimo sia riferito alla lettera o tutto il monomio. In questa lezione vedremo che cos’è per definizione il grado di un polinomio, iniziando proprio dai due casi da distinguere:

Grado complessivo di un polinomio

Per definizione il grado di un polinomio è il grado massimo dei monomi che lo compongono. Cioè tra tutti i monomi vediamo qual è quello con il grado più alto: quel numero sarà il grado complessivo di un polinomio. Vediamo subito un esempio:

Nell’esempio in figura notiamo che il monomio è composto da 3 monomi. Come già hai imparato nelle precedenti lezioni il grado di un monomio si calcola sommando gli esponenti, per cui il primo monomio ha grado 5, il secondo ha grado 7 e il terzo 9. Per cui il grado complessivo del polinomio è 9.

Grado del polinomio rispetto alla lettera

La definizione è estremamente semplice: è il grado massimo di ogni mononio rispetto a quella lettera. Quello che abbiamo visto nell’esempio è il grado complessivo del polinomio. Ma possiamo anche dire che il polinomio è di terzo grado rispetto alla lettera a, di quarto grado rispetto alla lettera b e di quarto grado rispetto alla lettera c.

Questo significa che il grado di un polinomio rispetto a una lettera è dato dal massimo esponente con cui compare la lettera all’interno del polinomio dato. Ovviamente il polinomio deve essere stato già ridotto nella sua forma normale, per cui si presumono già risolte le operazioni tra monomi.

Esempio sul grado di un polinomio

Ecco un bell’esercizio per mettere alla prova se le regole apprese fino ad ora sono chiare. Dell’espressione in basso dobbiamo cercare il grado del polinomio.

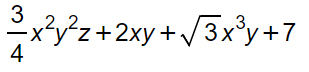
Essendo la prima volta che fai questo tipo di calcolo, ragioniamo in maniera semplificata facendo tutti i passaggi. Iniziamo quindi con il calcolo del grado dei vari monomi.

Monomio 1

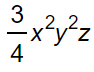
Per calcolarne il grado, basta fare la somma degli esponenti.

• x²→2
• y²→2
• z→1

Grado del monomio: 5

Monomio 2

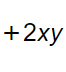
Anche in questo caso, basta trovare l’esponente di ogni lettera e poi farne la somma.

• x→1
• y→1

Grado del monomio: 2

Monomio 3 + termine noto

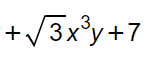
Come nei casi precedenti, senza lasciarsi spaventare dalla radice, vediamo solo l’esponente delle lettere. Il termine noto lo abbiamo riportato qui per completezza, ma non ha alcuna rilevanza ai fini del calcolo del grado del polinomio, visto che non avendo monomi, ha grado 0.

• x³→3
• y→1

Grado del monomio: 4

Il grado del polinomio è 5 perché è il massimo dei gradi di monomio calcolati.

Grado polinomio rispetto alla lettera x

Immaginiamo ora di voler capire, nello stesso esempio fatto prima, qual è il grado massimo rispetto alla x. Quello che possiamo notare è che nel primo monomio la x ha esponente 2, nel secondo ha esponente 1, nel terzo ha esponente 3. Questo vuol dire che:

il grado del polinomio rispetto alla lettera x è 3, perché è il massimo grado dei monomi.

Grado polinomio rispetto alla lettera y

Ripetiamo l’ultimo esercizio, ma questa volta la lettera è la y. Nel primo monomio ha esponente 2, nel secondo monomio ha esponente 1 così come nel terzo:

il grado del polinomio rispetto alla lettera y è 2, perché è il massimo grado dei monomi.

Grado polinomio rispetto alla lettera z

Analogamente si nota che l’esponente della lettera z è 1, 0, 0 rispettivamente nel I, II e III monomio. Per cui:

il grado del polinomio rispetto alla lettera z è 1, perché è il massimo grado dei monomi.

Riassumendo i dati dell’esercizio:

In definitiva possiamo dire che il polinomio:

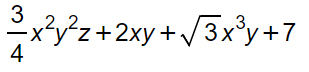
• ha grado complessivo pari a 5;
• di terzo grado rispetto alla x;
• di secondo grado rispetto alla y;
• di primo grado rispetto alla z.

Definizione di polinomio omogeneo

Concludiamo questa prima parte sugli appunti sul grado dei polinomi dando la definizione di polinomio omogeneo. Quando ci troviamo in presenza di un polinomio che abbia tutti i termini dello stesso grado, si parla di polinomio omogeneo. Ecco un esempio che ti aiuterà a chiarire la definizione appena esposta:

Il polinomio è omogeneo i terzo grado.

Prima di concludere ti diamo un ultima definizione, piuttosto banale. Un polinomio è ordinato quando gli esponenti sono messi in ordine decrescente. Il termine senza incognita viene definito in genere termine noto. Esempio:

Il polinomio in figura è di secondo grado, omogeneo ed ordinato secondo le potenze decrescenti di b, crescenti di a.

Se hai trovato questa lezione chiara e ti è stata utile, lascia un feedback positivo nei commenti. Se hai ancora dei dubbi o problemi, non esitare a scriverci le tue difficoltà. Il nostro staff ti risponderà nel minor tempo possibile.