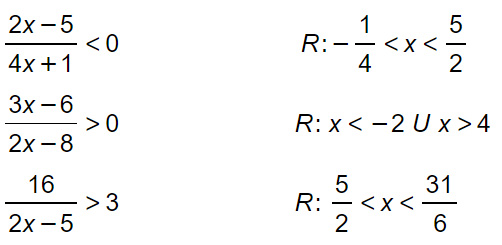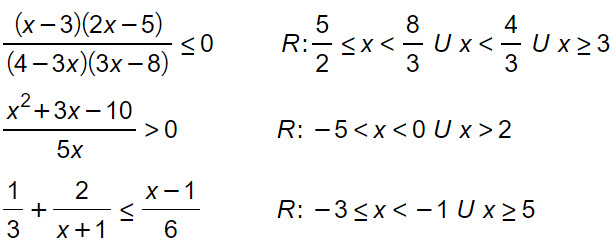Se stai cercando degli esercizi sulle disequazioni fratte di primo grado, ecco l’esercitazione completa sull’argomento. In questa pagina troverai tanti esercizi svolti con crescente livello di difficoltà grazie ai quali potrai imparare a risolvere le disequazioni fratte di qualsiasi tipo di difficoltà.
Come risolvere gli esercizi sulle disequazioni fratte
Prima di passare alle tracce degli esercizi, facciamo un breve riepilogo sulla tecnica di risoluzione. Tutte le disequazioni fratte, non importa il grado del polinomio, si risolvono sempre allo stesso modo. Ecco sintetizzati gli step da utilizzare in tutti gli esercizi:
- scomporre, se possibile, gli eventuali polinomi al denominatore di grado superiore al primo;
- calcolare il minimo comune multiplo tra tutti i denominatori;
- ricondursi alla forma canonica base delle disequazioni fratte:
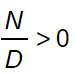
Ovviamente nella disequazione può esserci sia il simbolo maggiore, maggiore e uguale, minore o minore e uguale. Ai fini del calcolo cambia poco.
- Creare un “falso sistema” di disequazioni in cui si va ad imporre N>0 e D>0.
- Si mettono sul grafico le soluzioni delle due disequazioni e si sceglie il segno + o – a seconda del segno iniziale della disequazione N/D.
Disequazioni fratte esercizi
Risolvere le seguenti disequazioni fratte di primo grado.
Esercizio 1
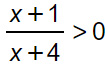
Svolgimento
In questo caso la traccia ci porta già alla situazione di avere un numeratore e un denominatore unici. Per cui possiamo già risolvere le due disequazioni separatamente:
N>0 → x+1>0
D>0 → x+4>0
Risolvendo queste due piccole disequazioni di primo grado, abbiamo come risultato:
x>-1
x>-4
Poniamo i risultati ottenuti sul grafico, valutandone i segni:
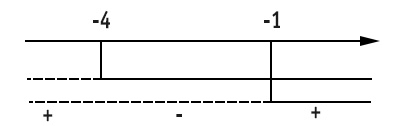
Poiché nella traccia dell’esercizio, la disequazione fratta ha il simbolo maggiore, prendiamo tutti gli intervalli con il segno positivo. Per cui il risultato corretto è:
x<-4 U x>-1
Esercizio 2
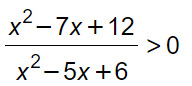
Svolgimento
Questa volta abbiamo un esercizio sulle disequazioni fratte di secondo grado. Per risolverla ripetiamo gli stessi passaggi dell’esercizio precedente. Per cui si impongono numeratore e denominatore maggiori di zero.
N>0 → x²-7x+12>0
D>0 → x²-5x+6>0
Si tratta di disequazioni di secondo grado che possono essere risolte con vari metodi: somma e prodotto, il calcolo del delta, … Iniziamo dalla prima:
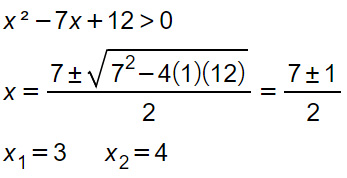
A questo punto poiché nella disequazione c’è il simbolo maggiore si prendono soluzioni esterne:
x<3 U x>4
Passiamo ora alla seconda disequazione del sistema.
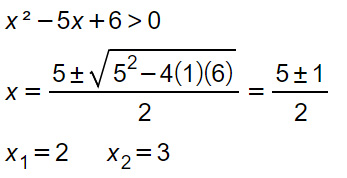
x<2 U x>3
A questo punto possiamo creare un grafico unico con le due soluzioni:
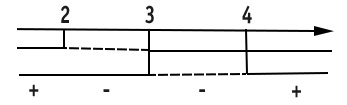
Poiché nella traccia dell’esercizio abbiamo N/D>0, prendiamo tutti i segni positivi. Per cui la soluzione finale è:
x<2 U x>4
Esercizio 3
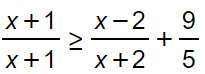
A differenza degli esercizi precedenti, questa volta abbiamo più numeratori e denominatori. Ovviamente la prima considerazione è che il termine (x+1)/(x+1) si può semplificare ed è pari a 1. Bisogna poi riportarsi alla forma N/D. Per farlo è necessario calcolare il minimo comune multiplo, che è in questo caso è semplice:
mcm = 5(x+2)
Portiamo tutto a primo membro, così da scrivere un denominatore unico:
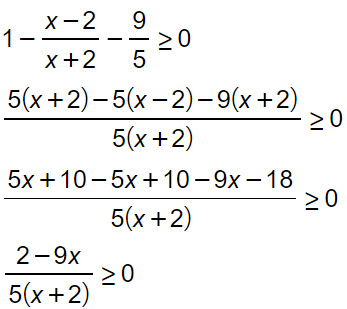
A questo punto possiamo dividere numeratore e denominatore:
N≥0 → 2-9x≥0
D>0 → 2(x+2)>0
OSSERVAZIONE: al denominatore il simbolo dell’uguale non va mai posto perché andrebbe a violare le condizioni di esistenza. Se non ricordi cosa sono, vai a rileggerti la lezione sulle equazioni fratte di primo grado.
x≤2/9
x>-2
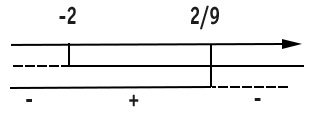
Poiché nella forma N/D abbiamo il simbolo maggiore e uguale, prendiamo le soluzioni con segno positivo, ricordandoci di riportare il simbolo uguale sulla frazione 2/9. Il risultato dell’esercizio è quindi:
-2<x≤2/9
Disequazioni fratte esercizi da risolvere