Le disequazioni di primo grado, sono delle disequazione che hanno al loro interno l’incognita x di grado 1. Proprio per questa ragione vengono chiamate anche disequazioni lineari.
Per poterle risolvere è necessario effettuare operazioni e semplificazioni così da ricondurre la disequazione di primo grado nella forma più semplice:
ax>b
(maggiore)
ax<b
(minore)
ax≥b
(maggiore e uguale)
ax≤b
(minore e uguale)
Come si risolvono le disequazioni di primo grado?
I valori a e b si chiamano coefficienti della disequazione e appartengono all’insieme dei numeri reali. Una volta giunti ad una delle quattro forme base viste sopra, possiamo risolvere esattamente come siamo abituati con le equazioni di primo grado. Quindi la x viene isolata portando il coefficiente a al denominatore del secondo membro.
ax>b → x>b/a
ax<b → x<b/a
ax≥b → x≥b/a
ax≤b → x≤b/a
Tutto quello che c’è da sapere sulle disequazioni di primo grado è finito. Tutte le difficoltà che potrai incontrare riguardano sostanzialmente i passaggi algebrici. Il difficile, in poche parole, è solo arrivare ad uno dei quattro casi visti sopra.
Quando prenderai confidenza con l’argomento passerai a dei casi un po’ più complessi, come le disequazioni di primo grado fratte, in cui l’incognita x compare anche al denominatore. Iniziamo intanto a concentrarci sui casi più semplici.
2 consigli per evitare di sbagliare
1) Se cambi i segni cambia anche il verso
La cosa fondamentale da ricordare è che nelle disequazioni di primo grado se vogliamo cambiare tutti i segni va cambiato anche il verso. Mentre cioè nelle equazioni di primo grado era sufficiente cambiare solo tutti i segni, qui dobbiamo ricordarci di trasformare il maggiore in minore e viceversa.
2) Disequazioni lineari con le frazioni
Nella nostra esperienza abbiamo avuto modo di constatare che gli studenti ci chiedono un aiuto soprattutto quando i coefficienti sono delle frazioni. Se invece di a e b abbiamo delle frazioni cosa succede? E’ un aspetto che abbiamo già evidenziato nelle equazioni di primo grado, ma è meglio ribadirlo piuttosto che avere dei dubbi. Facciamo subito lo schema di come risolvere:
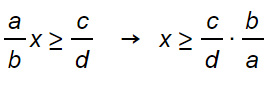
Come puoi notare è sufficiente trasportare la prima frazione (il coefficiente della x) al secondo membro come prodotto e capovolgerla: il numeratore diventa denominatore e viceversa. Seguendo questa regola non avrai più bisogno di aiuto e sicuramente eviterai dubbi o errori.
I primi esercizi con le disequazioni di primo grado
Quelli che ti proponiamo ora sono alcuni esercizi e problemi risolti con soluzione. Si tratta di esempi che potrai trovare utili per applicare i metodi di risoluzione visti sopra nella parte teorica. Vediamo allora come si risolvono le disequazioni di primo grado seguenti.
Esempio 1
3x-4>0
Abbiamo detto che per risolvere una disequazione di 1 grado bisogna isolare la x al primo membro. Per cui il termine noto (cioè i coefficiente senza la x) va portato al secondo membro cambiandogli il segno.
3x>+4
A questo punto, per isolare definitivamente la x, bisogna portare il coefficiente 3 al secondo membro. Dividiamo quindi primo e secondo membro della disequazione lineare per 3.
x>+4/3
Esempio 2
3x+4≥3(x+2)-2
Rispetto al caso precedente c’è semplicemente una moltiplicazione in più da eseguire. Risolviamo subito il prodotto per eliminare la parentesi tonda:
3x+4≥3x+6-2
3x+4≥3x+4
Portiamo quindi ora tutti i monomi con la x al primo membro, mentre i termini noti vanno al secondo membro.
3x-3x≥+4-4
0x≥0
Abbiamo ottenuto un risultato decisamente strano. Poiché 0 moltiplicato per x fa 0, la disequazione ci sta chiedendo quando 0≥0? Se la disequazione fosse con il segno > (solo maggiore) sarebbe impossibile, perché 0 non è maggiore di se stesso. In questo caso, tuttavia, la disequazione di primo grado ha il verso maggiore e uguale. Poiché 0=0, allora il risultato è sempre verificato. In matematica si scrive come:
∀x∈R
Si legge per ogni x appartenente ad R che equivale a dire che qualsiasi valore noi assegniamo alla x, il risultato è sempre valido.
Esempio 3
√2 x +1≥ 3+x
Si tratta di una disequazione di primo grado a coefficiente irrazionale. Cioè uno dei coefficienti è una radice quadrata. Senza lasciarci prendere dal panico, applichiamo il metodo risolutivo: i coefficienti con la x al primo membro, tutti gli altri al secondo membro.
√2 x≥ 3-1
√2x ≥ 2
x ≥ 2/√2
A questo punto possiamo applicare la regola delle razionalizzazioni dei radicali. Moltiplichiamo e dividiamo il secondo membro per √2.
x ≥ 2/√2 · √2/√2
x ≥ 2√2/2
x ≥ √2.
Esempio 4
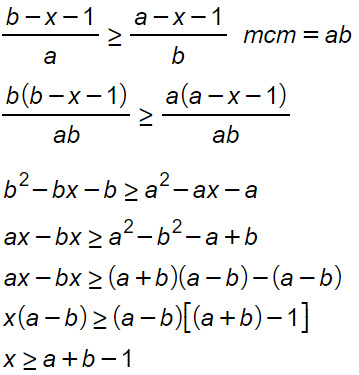
Questo ultimo esercizio può sembrare più difficile ma chiarisce quanto le disequazioni di primo grado siano in realtà semplice. Può essere l’espressione in sé più complessa, ma il metodo risolutivo è sempre lo stesso. In questo caso abbiamo sfruttato la tecnica di semplificazione dei polinomi del raccoglimento a fattor comune per ottenere il binomio letterale (b-a) sia a primo che a secondo membro.
Conclusioni
Riepilogando: in questa lezione abbiamo visto come si fanno le disequazioni di primo grado analizzando le varie casistiche. Ci siamo imbattuti in esercizi con le frazioni, con le radici e addirittura con le lettere. Sei sei stato in grado di seguire e risolvere con noi questi esempi? Se questa lezione ti è stata chiara o se hai ancora dubbi o necessiti di chiarimenti, lascia un commento qui in basso. Il nostro staff ti risponderà nel minor tempo possibile.