Il calcolo del rapporto incrementale è fondamentale, almeno in un primo momento, per capire che cos’è e come si definisce la derivata prima di una funzione. Visto che genera molte difficoltà a tanti studenti, in questa lezione vedremo in maniera semplice che cos’è il rapporto incrementale e come si può calcolare con pochi semplici passaggi.
Definizione di rapporto incrementale
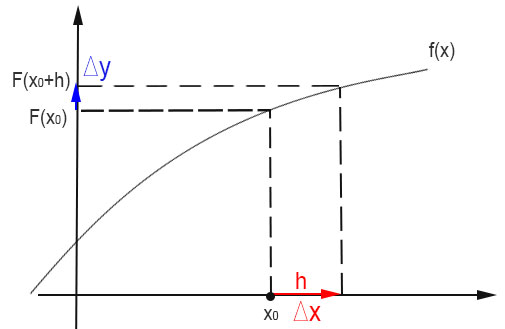
Data sul piano cartesiano la funzione f(x), consideriamo un suo generico punto x0 appartenente al dominio della funzione.
Il rapporto incrementale è pari al rapporto tra la variazione di ordinate e la variazione di ascisse, considerando un incremento h. Vale quindi la formula:
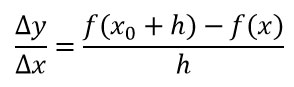
CI HAI CAPITO POCO? ECCO LA SPIEGAZIONE SEMPLICE!
Data la funzione f(x), si considera il suo punto x0 a cui aggiungiamo una certa quantità h. Quindi a x0 passiamo a x0+h. La distanza tra i due punti (0;x0) e (0;x0+h) è pari proprio ad h, come si vede anche in figura. La variazione di x, chiamata Δx, è pari ad h.
Sull’asse delle ordinate, invece, si parte dal punto f(x0) e, a seguito dell’incremento h, si ottiene il punto f(x0+h). Quindi la variazione di ascissa è Δy ed è pari f(x0+h)-f(x0).
In base alla definizione vista, il rapporto incrementale è proprio il rapporto tra queste due quantità Δy/Δx. Il nome è dovuto al fatto che si tratta di una divisione di due quantità generate a seguito di un incremento (h).
Significato geometrico del rapporto incrementale
Abbiamo quindi capito, in termini di definizione e di formula, che cos’è il rapporto incrementale. Cerchiamo ora di capire che cosa rappresenta in termini geometrici sugli assi cartesiani questa quantità, partendo proprio dal disegno visto in alto. Ridisegniamo due segmenti Δx e Δy come nella figura che segue, così da ottenere il triangolo rettangolo ABC. In particolare Δx=AB e Δy=BC.
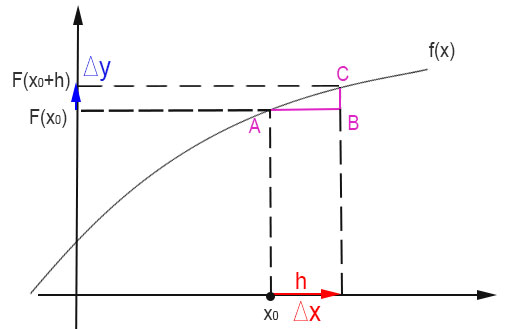
Ti ricordi i teoremi sui triangoli rettangoli in trigonometria? Ne hai senz’altro studiato uno che recita:
In un triangolo rettangolo, un cateto è uguale all’altro cateto per la tangente dell’angolo opposto.
Questo vuol dire che il cateto CB è uguale al cateto AB per la tangente dell’angolo in A. Cioè vale la formula:
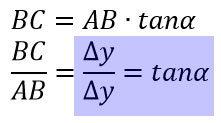
Abbiamo quindi scoperto che il rapporto incrementale geometricamente è la tangente dell’angolo nel punto della funzione [x0, f(x0)]. Questo sarà il punto di partenza per capire proprio il significato geometrico della derivata.
Rapporto incrementale esercizi svolti
Proviamo a mettere in pratica quello che abbiamo visto fino a questo momento con qualche applicazione pratica ed esempio di calcolo. Una delle domande che più ci arrivano dai nostri studenti riguarda il rapporto incrementale della funzione fratta.
ESERCIZIO 1
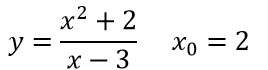
Considerando sempre l’incremento h e visto che x0=2, allora l’espressione (x+h) diventa (2+h). Quindi risolviamo esplicitando tutti i passaggi:
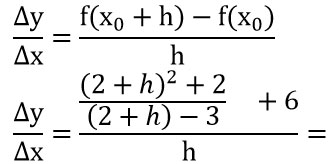
Come puoi vedere alla f(x0+h) abbiamo sostituito la funzione fratta assegnata dalla traccia mettendo 2 al posto di x0. Il termine f(x0) diventa immediatamente pari a 6. Risolviamo il quadrato di binomio al numeratore:
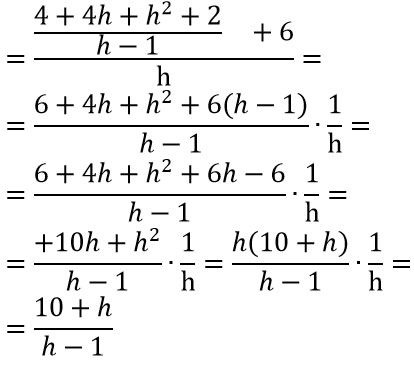
Il calcolo del rapporto incrementale quindi si è ridotto ad una serie di semplici passaggi algebrici per ottenere alla fine una funzione di h. Quando dovrai calcolare la derivata, semplicemente dovrai aggiungere il calcolo di un limite che si ridurrà nella maggior parte dei casi ad una semplice sostituzione.
ESERCIZIO 2
Questo secondo esempio è con la funzione logaritmo: semplicemente, come nell’esercizio precedente, andiamo a sostituire il punto x0=2 all’interno della formula definizione di rapporto incrementale.
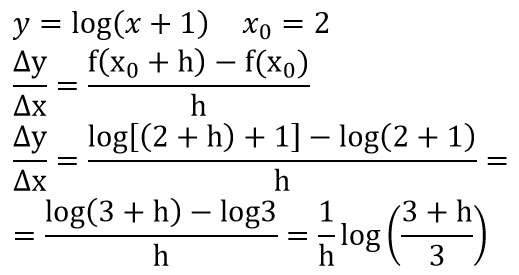
Al numeratore abbiamo utilizzato le proprietà dei logaritmi, così il tre passa al denominatore all’interno del logaritmo.
ESERCIZIO 3
Se sei arrivato a studiare questo argomento, vuol dire che sai già come si risolvono i limiti. Cerchiamo allora di risolvere insieme il calcolo della derivata della funzione quadratica y uguale x al quadrato. Si tratta dell’equazione di una parabola con vertice nell’origine di cui andremo a calcolare il rapporto incrementale e alla fine applicheremo il limite per h che tende a 0.
Unica nota di questo esercizio: lasciamo x0 generico indicandolo come x. Ma vediamo assieme come si risolve passo passo:
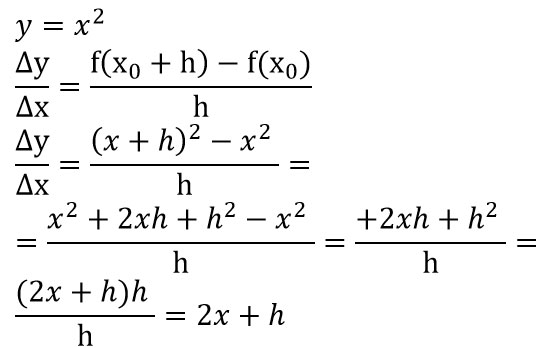
A questo punto applichiamo il limite per h che tende a 0. Sostituendo cioè 0 al posto di h, si ottiene immediatamente il risultato finale: 2x. Come studieremo nelle prossime lezioni, la derivata del quadrato di x è proprio pari a 2x. Ecco ora hai imparato anche a fare la tua prima derivata con il metodo del rapporto incrementale!