L’equazione della parabola parabola nel piano cartesiano è un’equazione di secondo grado del tipo:
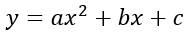
In realtà, come vedremo in questa lezione, le posizioni delle variabili x e y dipendono dalla disposizione della figura negli assi cartesiani. Oltre all’equazione della parabola generale, vedremo anche come si calcolano elementi caratteristici di questa figura geometrica come vertice, asse, fuoco e direttrice.
In base alla posizione dell’asse della parabola, la formula può cambiare ed è proprio per questa ragione che possiamo distinguere i due seguenti casi.
CASO 1
Equazione parabola con asse parallelo all’asse y
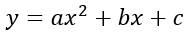
dove:
- a>0 nel caso di parabola rivolta verso l’alto
- a<0 nel caso di parabola rivolta verso il basso

In questo primo caso la parabola con asse verticale. Infatti nelle formule viste in alto ci accorgiamo come l’asse di simmetria sia rappresentato dall’equazione di una retta verticale.
Possiamo inoltre notare come sia nelle coordinate del vertice, che in quelle del fuoco e della direttrice compare un termine b al quadrato meno 4 a c. Ti ricordi che lo avevamo già incontrato quando abbiamo studiato le equazioni di secondo grado? Si, è proprio la formula del delta!
CASO 2
Equazione parabola con asse parallelo all’asse x
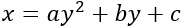
dove:
- a>0 nel caso di parabola rivolta verso destra
- a<0 nel caso di parabola rivolta verso sinistra

Formule sulla parabola (suggerimenti per gli esercizi)
#TIPS: Come trovare equazione parabola?
In questa sezione raccogliamo alcune formule ed equazioni che ti saranno sicuramente utili per risolvere alcuni particolari esercizi.
Equazione parabola passante per tre punti
E’ uno degli esercizi più frequenti della geometria analitica: trovare l’equazione di una figura passante per 2 o 3 punti. Abbiamo infatti già incontrato una lezione su come si determina la retta per due punti e la circonferenza per tre punti.
Il procedimento è del tutto analogo: si costruisce un sistema in cui si sostituiscono le coordinate dei punti all’interno dell’equazione di una parabola generica. Dati cioè tre punti:
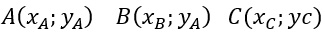
Li inseriamo nella formula della parabola:
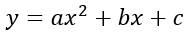
così da ottenere un sistema di 3 equazioni nelle tre incognite a, b e c.
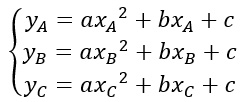
Equazione parabola passante per 2 punti
Anche dal punto di vista grafico, una parabola è univocamente determinata solo se si hanno a disposizione 3 punti. Ne bastano invece soltanto 2 se uno di questi è il vertice, la direttrice o il fuoco.
Equazione parabola con vertice e punto P: se abbiamo le coordinate del vertice, le sostituiamo all’interno della formula del calcolo del vertice. In questo modo otteniamo due equazioni.
Ad esempio:
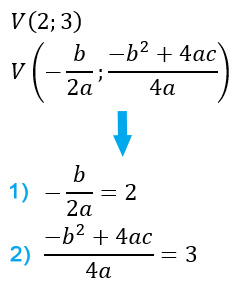
Si sfrutta infine l’appartenenza del punto P alla figura. Come? Semplicemente sostituendo le sue coordinate nell’equazione della parabola generica.
Ad esempio:
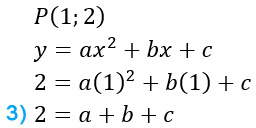
A questo punto si prendono le 3 equazioni che abbiamo segnato, le si mette in un sistema (che sarà quindi composto da 3 equazioni nelle 3 incognite a,b e c) e ho trovato l’equazione della parabola richiesta.
Equazione parabola noto il fuoco e un punto P: il procedimento è perfettamente analogo al caso precedente. Questa volta invece di utilizzare la formula del vertice, utilizzeremo quella del fuoco e faremo la stessa identica sostituzione.
Equazione della parabola con fuoco e direttrice
In questo caso abbiamo una parabola passante per un 1 punto (il fuoco) e la direttrice. Dagli esempi precedenti abbiamo visto che andando a sostituire le coordinate note di F all’interno della formula del fuoco, otteniamo 2 equazioni.
Esempio:

La terza e ultima equazione la otteniamo imponendo l’uguaglianza tra l’equazione della direttrice nota dalla traccia e la sua formula generica:
Esempio:
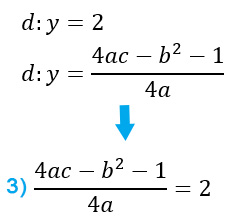
Anche in questo caso è sufficiente imporre un sistema con le tre equazioni per arrivare rapidamente alla soluzione.
Conclusioni
Abbiamo visto durante questa lezione che per determinare univocamente la formula della parabola sono necessarie 3 condizioni così da imporre un sistema di equazioni dove le incognite sono sempre a, b e c.
Se ti è tutto chiaro dovresti essere in grado di risolvere qualsiasi tipo di esercizio del tipo “trovare l’equazione della parabola noti …”.
Se appunti, formule ed esempio ti sono state d’aiuto o vorresti approfondire un’altra tematica, lasciaci un commento qui in basso. Ci aiuterai a migliorare ogni giorno la qualità delle nostre lezioni.
Prof.Paolo,;
ovviamente la lezione è nella tradizione didattica dell’argomento! Mia nipote che è curiosa mi avrebbe chiesto” nonno, quella formula che hai scritto, per ex; (X^2-2X-3)= Y) come si è formata?”
Perché poi la uguagli a zero? E se non la eguaglia zero che significato ha quella espressione che chiami polinomio?
Allora prof. le domande implicano delle risposte che non si possono differire con ” lo vedremo più avanti etc”
E’ da qui che bisognerebbe iniziare la lezione, precisando all’allievo che ha già gli elementi primordiali per comprendere il significato del grafico che rappresenta un polinomio,proprio come quello più sopra che è il prodotto di due binomi (x-3)(x+1)=(x^2+x-3x-3)=(x^2-2x-3).
Qui si deve rammentare allo studente che se uguagliamo il polinomio-funzione =0 otteniamo
sia ,nella forma (x-3)(x+1)=0 le due radici : x=3 e x=(-1) ed anche nella forma della funzione
eguagliata a zero; x^3-2x-3=0 >> le cui radici si ottengono applicando il determinante :
x=[ -(-2)±√ (-2)^2 -( 4*1*(-3)]/2 = (2±4)/2 = (x=+3) e (x=(-1)
ma occorre spiegare il significato e l’ordine di (x^2-2x-3) ; qui dobbiamo tornare a Pitagora e ipotizzare che il Maestro sia pervenuto alla identità che gli è attribuita .
Egli aveva ben compreso le proprietà dei numeri naturali e lo sviluppo di esse.
Immaginò che la Serie dei numeri dell’insieme N è una somma di parti della Serie medesima e scrisse che occorreva sviluppare le possibilità di una terna di numeri >>(n) ;(n+1) e (n+2) considerando i loro quadrati tali che la somma dell’ultima sia la somma dei due che lo precedono; dunque (n^2)+(n+1)^2=(n+2)^2; che sviluppati ,ordinati ed uguagliati a zero dànno >>
n^2-2n-3=0 . Naturalmente si farà osservare allo studente che( n )ha lo stesso significato di( x)
solo che n è un numero sulla retta dei Numeri naturali o dell’insieme N mentre( x )è l’incognita che viene risolta con la funzione che ,uguagliata a zero, diventa equazione ma soprattutto x è l’evidenza che abbiamo avuto bisogno di un sistema di riferimento di assi cartesiani per rappresentare la posizione delle coordinate sull’asse X dove Y=0.
Sono persuaso che gli studenti più curiosi(meno pigri) avranno un altro approccio alla matematica.
Cordialità.
Torino,li, 11 febbraio 2022
joseph